Oxford Entrance Exam Problem 7

Algebra Level 3

y = 2 x 2 − 4 x + 3 \LARGE y=2^{x^2-4x+3}

How can the graph of the function above be obtained from the graph of y = 2 x 2 y=2^{x^2} ?

a translation parallel to the x-axis followed by a stretch parallel to the y-axis. reflection in the y-axis followed by translation parallel to the y-axis. a translation parallel to the x-axis followed by reflection in the y-axis. a stretch parallel to the y-axis followed by a translation parallel to the y-axis. a translation parallel to the x-axis followed by a stretch parallel to the x-axis.

View wiki
A Former Brilliant Member by A Former Brilliant Member

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

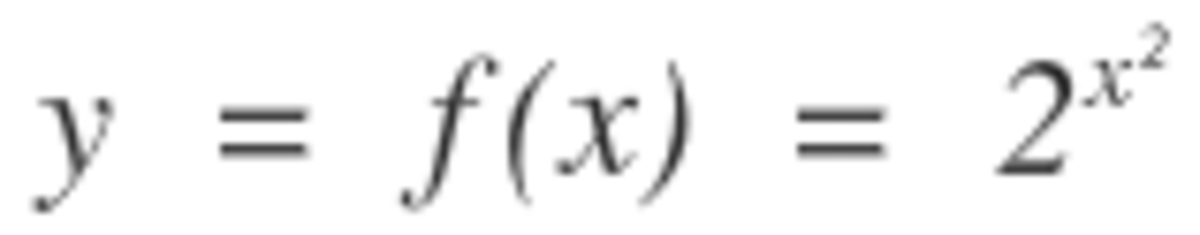
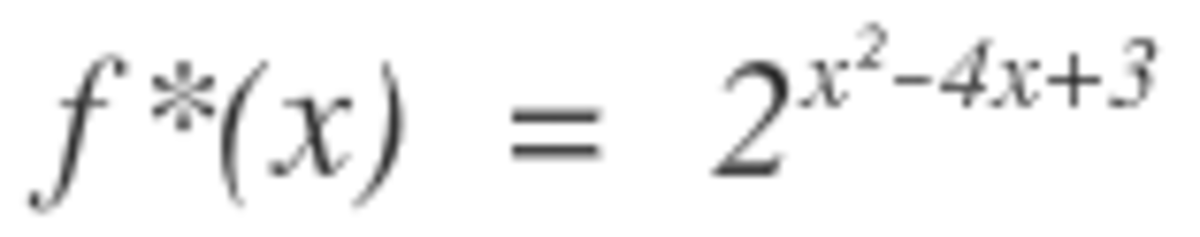
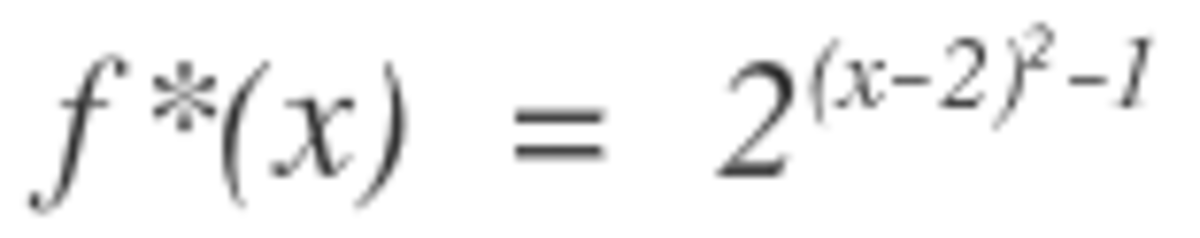
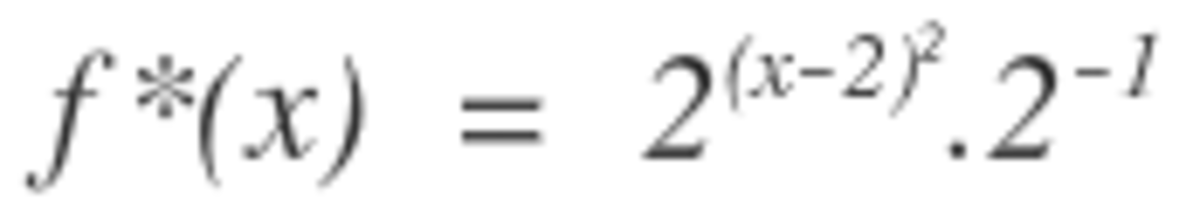
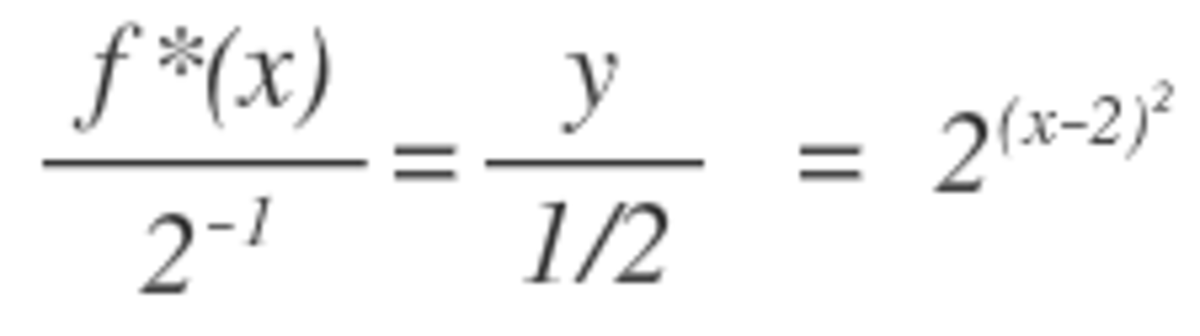
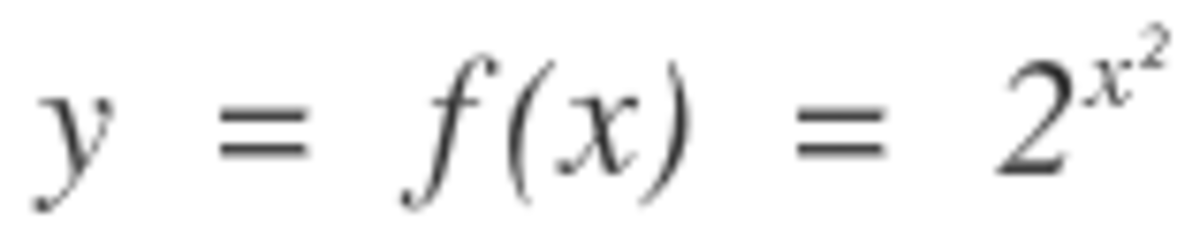
With f ( x ) = 2 x 2 f(x) = \large 2^{x^{2}} we have that g ( x ) = 2 x 2 − 4 x + 3 = 2 ( x − 2 ) 2 − 1 = g(x) = \large 2^{x^{2} - 4x + 3} = 2^{(x - 2)^{2} - 1} = 1 2 f ( x − 2 ) . \dfrac{1}{2}f(x - 2).

Thus to obtain g ( x ) g(x) we must shift f ( x ) f(x) to the right by 2 2 units, (i.e., a translation parallel to the x x -axis), followed by a "halving" of the shifted y y values, (i.e., a stretch parallel to the y y -axis).

9 Helpful 0 Interesting 0 Brilliant 0 Confused

Let

We need to obtain

Completing the square, ; Simplifying,

So,

When we compare this with We see that, this function has been obtained by : Translating right by 2 units - a translation parallel to the x axis Stretching vertically by 1/2 units - a stretch parallel to the y axis

2 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...