Pack Away

Geometry Level 5

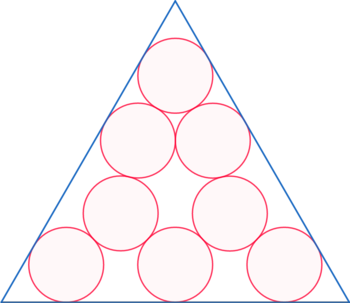
The figure shows eight identical circles packed in an equilateral triangle.

Packing Efficiency = Total area of the packing material Total area of the container \text{Packing Efficiency}=\dfrac{\text{Total area of the packing material}}{\text{Total area of the container}}

What is the packing efficiency in this case?

65.6 % 65.6\,\% 56.1 % 56.1\,\% 71.3 % 71.3\,\% 58.7 % 58.7\,\% 75.5 % 75.5\,\% 67.2 % 67.2\,\%

Digvijay Singh by Digvijay Singh , 21, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

In 1993 Melissen has proved that s the sides of an equilateral triangle that pack 8 unit circles is s=9.293. My calculations below are based on this.
s = 2 + 2 3 + 2 ∗ 33 3 = 9.293... ∴ a r e a o f t h e e q u i l a t e r a l Δ = 3 4 ∗ 9.29 3 2 . A r e a o f 8 u n i t ◯ = 8 π . η = 8 π 3 4 ∗ 9.29 3 2 ∗ 100 = 67.2 % . s =2+2\sqrt3+\dfrac{2*\sqrt{33} } 3 = 9.293...\therefore~area~of~the~equilateral~\Delta=\dfrac{\sqrt3} 4*9.293^2.\\ Area~of~8~unit~\bigcirc~=~8\pi.\\ \eta =\dfrac{8\pi}{\frac{\sqrt3} 4*9.293^2}*100 = 67.2 \%.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...