Packing a Pair of Ellipses
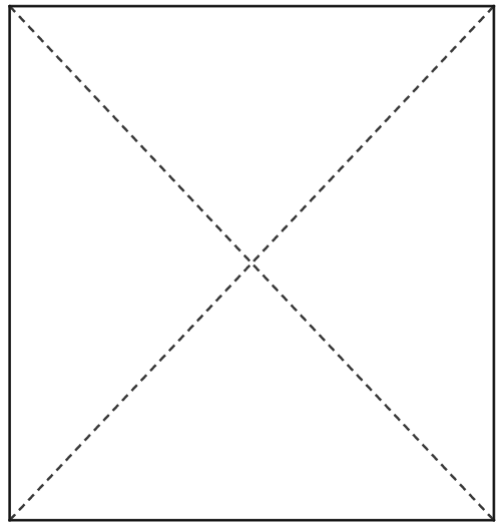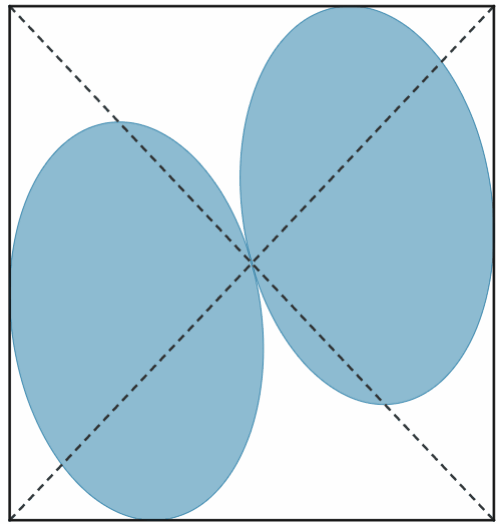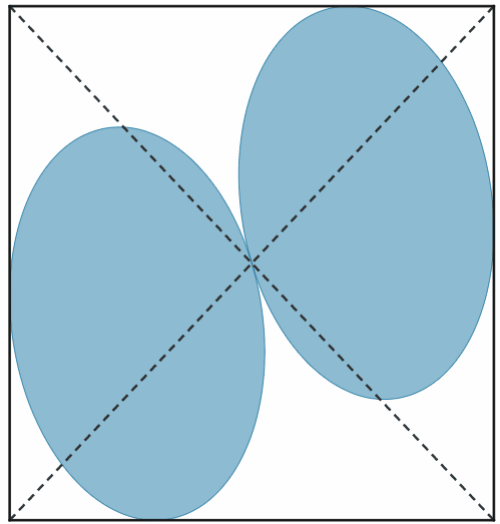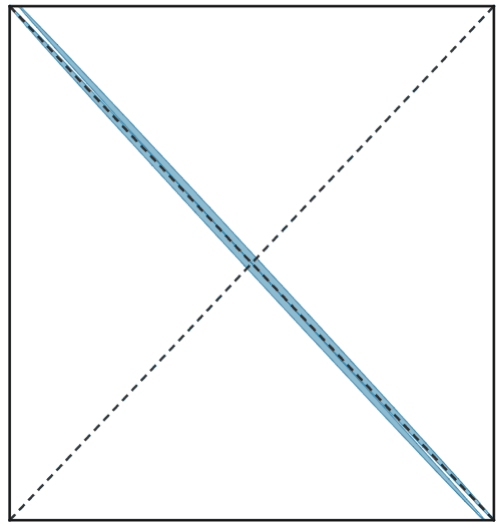 Two non-overlapping and equal ellipses of
eccentricity
e
are to be packed in a
unit
square such that they occupy the maximum possible area. The given animation shows the optimal packing for different values of
e
as
e
varies between
0
and
1
.
Two non-overlapping and equal ellipses of
eccentricity
e
are to be packed in a
unit
square such that they occupy the maximum possible area. The given animation shows the optimal packing for different values of
e
as
e
varies between
0
and
1
.
There is a critical number e 0 such that for 0 < e ≤ e 0 , the optimal packing occurs when the ellipses are symmetric about the diagonals of the square. However, for e 0 < e < 1 , the optimal packing is not symmetric about the diagonals. Find the distance between the centers of the two ellipses corresponding to the case e = e 0 .
The answer is n l m − l for coprime integers l , m , n . Submit l + m + n .
Hint: Study the following paper: Optimal packings of two ellipses in a square
The answer is 19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Place the unit square so that its vertices are at ( ± 2 2 , ± 2 2 ) , so that the edges are represented by the lines y = ± x ± 2 2 , and let the ellipses have semi-major axes of a and a semi-major axes of b with centers at ( ± b , 0 ) so that they are represented by the equations b 2 ( x ± b ) 2 + a 2 y 2 = 1 .
According to the paper in the given hint, the aspect ratio E 0 of each ellipse is E 0 = 1 1 6 3 − 3 = b a , so a 2 = 1 1 ( 6 3 − 3 ) b 2 , and substituting this into the equation of the ellipse on the right and rearranging gives 1 1 ( x − b ) 2 + ( 6 3 − 3 ) y 2 = 1 1 b 2 .
To be tangent to the line y = − x + 2 2 , the ellipse 1 1 ( x − b ) 2 + ( 6 3 − 3 ) y 2 = 1 1 b 2 will intersect it at only one x-value, so the discriminant of 1 1 ( x − b ) 2 + ( 6 3 − 3 ) ( − x + 2 2 ) 2 = 1 1 b 2 will be 0 . In other words, 2 2 b 2 + 1 2 6 b − 6 2 b − 6 3 + 3 = 0 , which solves to b = 2 2 6 2 − 6 .
The distances between the centers of the two ellipses is then 2 b = 1 1 6 2 − 6 , so l = 6 , m = 2 , n = 1 1 , and l + m + n = 1 9 .
a b = E 0 = 1 1 6 3 − 3 ≈ 0 . 8 1 9 8 ( 1 ) where a and b are the semi-major axis and the semi-minor axis of the ellipse.
As seen in the figure, point A lies on the director circle of one of the two ellipses, i.e. on a circle that has the same center O 1 as the ellipse and with radius r = a 2 + b 2 ( 2 )
Combining relations ( 1 ) and ( 2 ) we get r = ( E 0 b ) 2 + b 2 = b E 0 1 + E 0 2 Furthermore,
[ A B D ] = 2 1 A K ⋅ B D = 2 1 A B ⋅ A D ⇒ A K ⋅ B D = A B 2 ⇒ ( r + b ) 2 = 1 ⇒ ( b E 0 1 + E 0 2 + b ) 2 = 1 ⇒ 2 b ( E 0 1 + E 0 2 + 1 ) = 2 ⇒ 2 b = 1 + E 0 2 + E 0 2 E 0 Plugging the value of E 0 , we find that the distance between the centers of the two ellipses is ∣ ∣ O 1 O 2 ∣ ∣ = 2 b = 1 1 6 2 − 6 For the answer, l = 6 , m = 2 , n = 1 1 , thus, l + m + n = 1 9 .