Packing circles in square

What is the minimum side length of a square which can contain 5 non-overlapping unit circles?
Give your answer to 3 decimal places.
The answer is 4.828.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I think the image where we see the pink square and the purple circles is not precise in the intersection points.
Log in to reply
Yes, that is true (and I was lazy). I've added a slightly better diagram.
The image was drawn up for s being very close to T . The 4 circles will contain the origin (as opposed to having the origin lie on the circles as in the image).
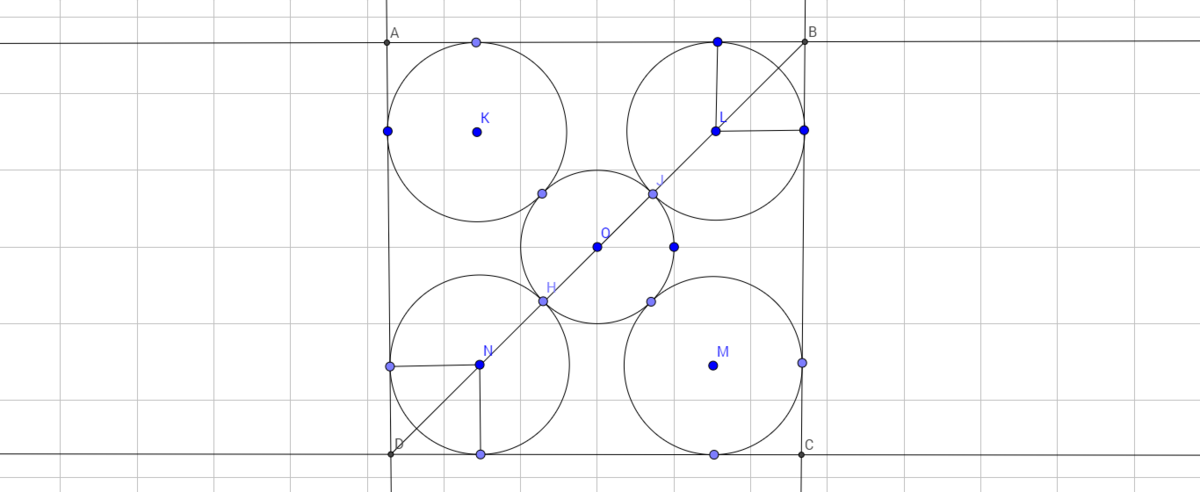 We can arrange the
5
circles as shown in the figure to attain minimum side length of the square.
We can arrange the
5
circles as shown in the figure to attain minimum side length of the square.
So now lets calculate the side length of the square. To do so, we join the points
B
,
L
,
J
,
O
,
H
,
N
,
D
which forms the diagonal.
We know
J
H
=
2
,
N
H
=
L
J
=
1
and
N
D
=
B
L
=
1
2
+
1
2
=
2
.
so the length of the diagonal
=
4
+
2
2
.
Therefore the side length of the square
=
2
D
i
a
g
o
n
a
l
=
2
4
+
2
2
=
2
2
+
2
≈
4
.
8
2
8
.
Although I'll agree that it's intuitive, the solution doesn't show why the arrangement shown leads to the minimal square area.
Log in to reply
Actually I tried out Many cases for it to be minimum.This was the arrangement I got then
Nice SOLUTION ( + 1 ) . I got it wrong because I found the area of the smallest rectangle that can accommodate this. LOL. Gonna post that as a question.
Log in to reply
well it is asked to find the side length of the square not rectangle. Thanks
Ah, nice follow up, Rohit! :)
What if the radius of circle is smaller than 1?
Log in to reply
He has taken 1 because it is the question's demand. It is true for every positive real. You can put there a variable.
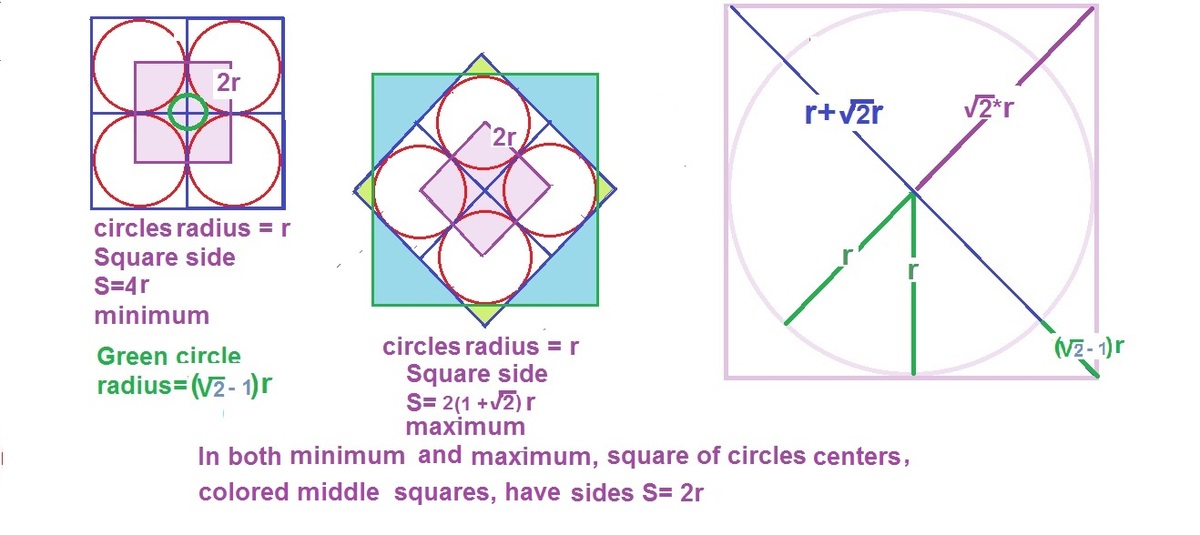 I have no proof to justify but my intuition is that at minimum or maximum, there is likely to be some symmetry. This would be so at least with 4 and five circles in a square. Rest is simple calculations. Circles should be tangential to other circle(s) or/and side(s).
Diagrams to understand the problem better
I have no proof to justify but my intuition is that at minimum or maximum, there is likely to be some symmetry. This would be so at least with 4 and five circles in a square. Rest is simple calculations. Circles should be tangential to other circle(s) or/and side(s).
Diagrams to understand the problem better
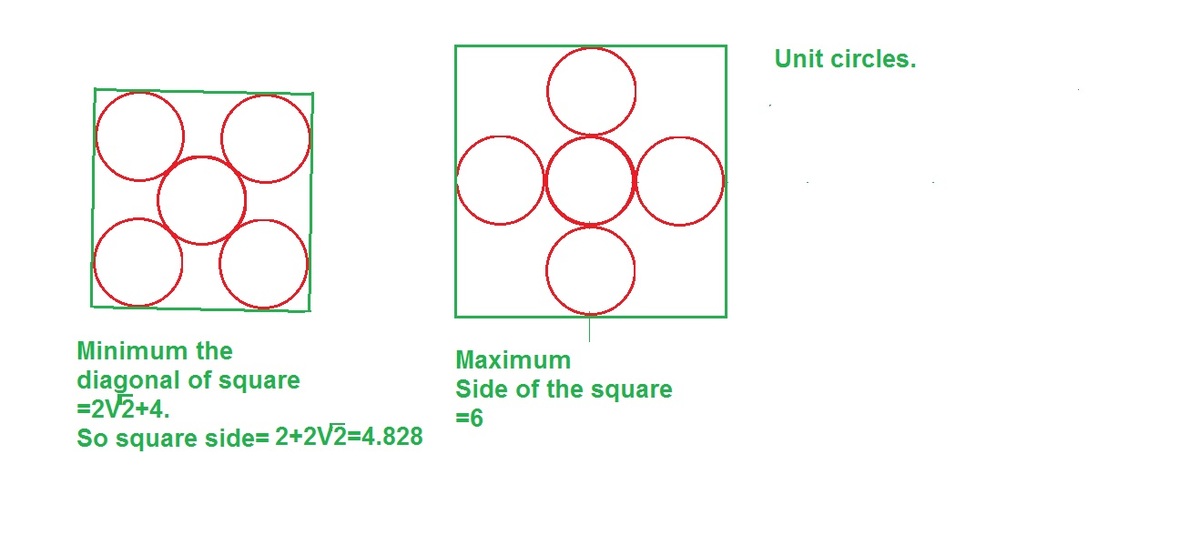
The image on the right gives a construction for 5 circles being placed in a square of side length T = 2 + 2 2 ≈ 4 , 8 2 8 . Thus, the answer is at most 4.828.
We now show that for 2 ≤ s < 2 + 2 2 , we can fit at most 4 circles into the square.
First, refer back the the image. Let the center of the square be the origin. Let's look at the tangential points of these circles (the purple points). The coordinates are given by ( ± 2 2 , ± 2 2 ) .
Now, for any square of side length s < 2 + 2 2 , let's also center the square at the origin. Consider the 4 points given by ( ± T s × 2 2 , ± T s × 2 2 ) , where we've scaled the image down by T s .
Claim: Any unit circle must contain one of these 4 points.
Proof: The vertices of the square are ( ± 2 s , ± 2 s ) .
The center of the unit circle lies distance 1 away from the sides of the square, so the center lies within the pink square with vertices ( ± ( 2 s − 1 ) , ± ( 2 s − 1 ) ) .
WLOG, say the center lies in the upper right quadrant. Then, since the circle with center ( T s × 2 2 , T s × 2 2 ) and radius 1 (the purple circle) will cover the entire upper right quadrant of the pink square , hence this implies that the center is distance < 1 from this point, which implies that the point lies within this circle.
Since there are only 4 points, and each unit circle must contain one of these points, thus we conclude that there are at most 4 unit circles in a square of side length s . □
This establishes that
1. T = 2 + 2 2 allows us to have 5 squares,
2. s < T does not allow us to have 5 squares.
Thus, T is the minimum.