Packing Efficiency
I have packed 4 equal circles, symmetrically placed inside a larger circle
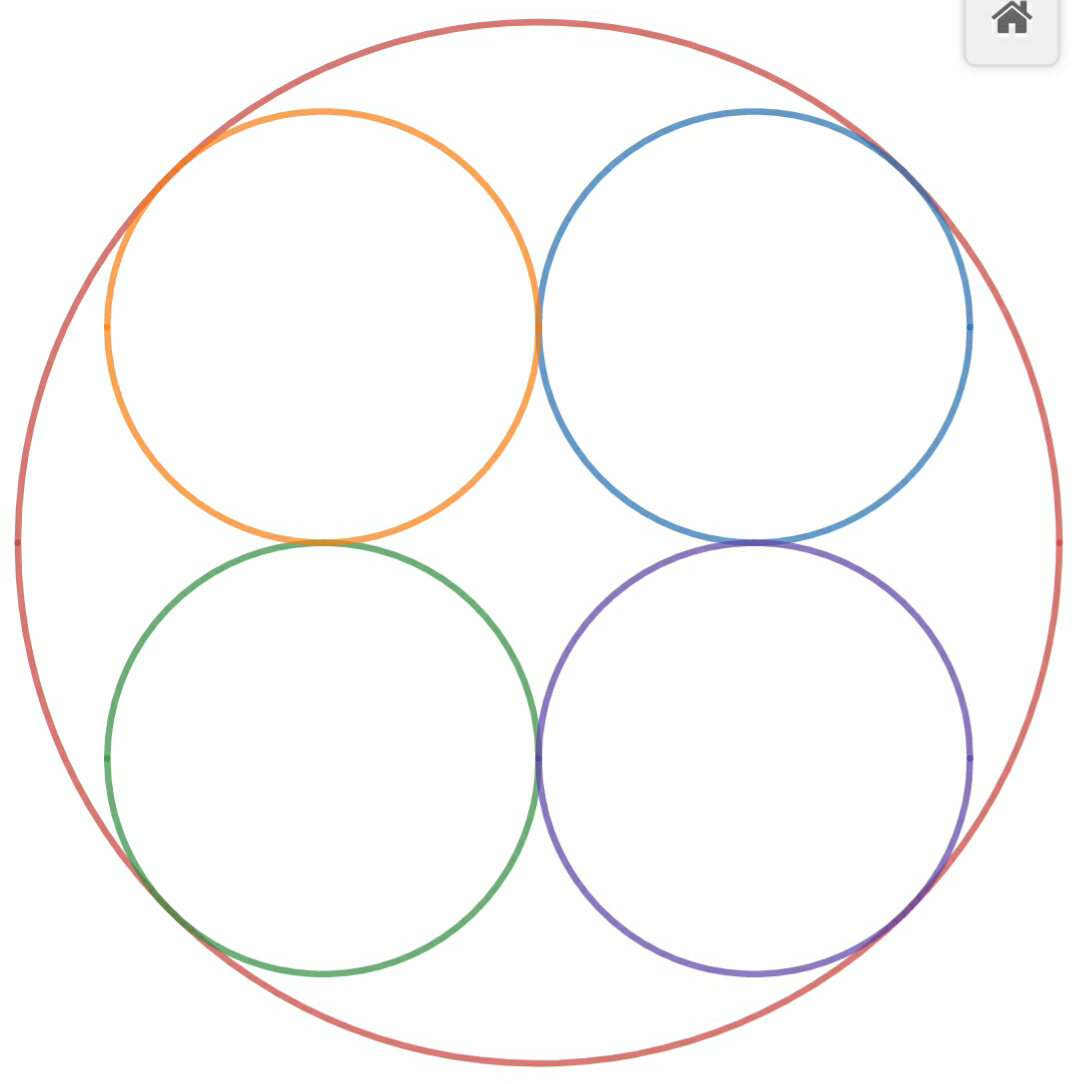
To the nearest two decimals, can you tell me the percentage packing efficiency of this setup?
As a further extension, I would like to discuss that if the same 2D figure is extended to 3D, that is, if there are four equal smaller spheres placed symmetrically inside a larger sphere, would the packing efficiency of that setup be more, less, or the same as the figure we found above?
The answer is 68.63.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the radius of the 4 equal circle be r and the radius of the large circle be R . Drawing the radii to the points of contact of the circles, we note that the centers of the four equal circles are the vertexes of a square of side length 2 r . We note that R = ( 1 + 2 ) r . Therefore, the packing efficiency is μ = π R 2 4 π r 2 = ( 1 + 2 ) 2 4 ≈ 6 8 . 6 3 % .