Packing Sangaku
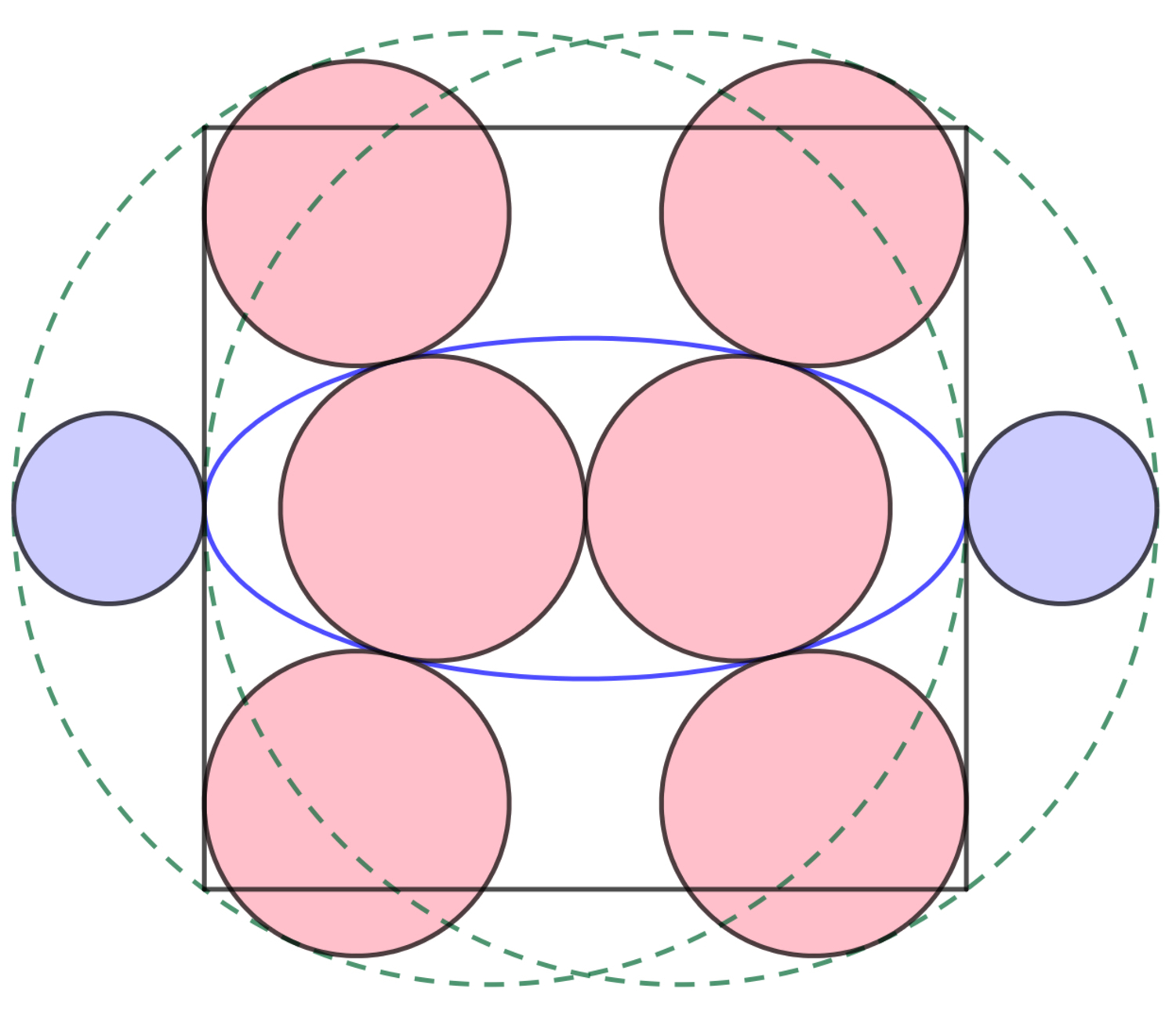
Each of the six pink circles - two inscribed in the ellipse and four outside - is pairwise-tangent to each other. Those four circles are also tangent to the dashed circles. The square is positioned symmetrically, so that it is tangent to both dashed circles, the ellipse and four pink circles. Two violet circles, both tangent to the square and the dashed circle, are each positioned centrally at the opposite side.
If the ratio of the radius of the violet circle to the radius of the dashed circle is R , input ⌊ 1 0 5 R ⌋ as your answer.
The answer is 20000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
That's how I did it, as well! That's what I call a Brilliant solution
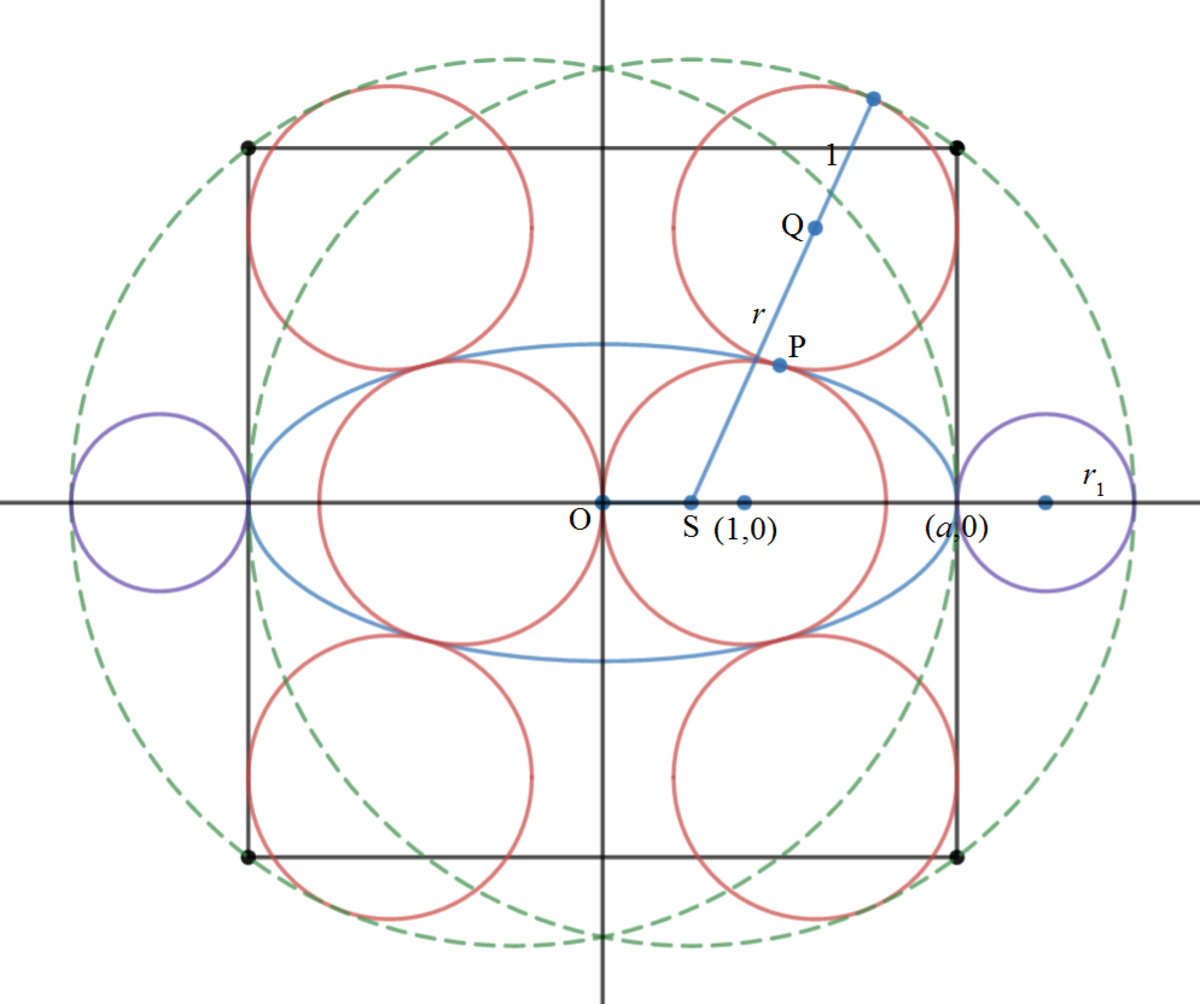
Let the center of symmetry of the figure be the origin O ( 0 , 0 ) of the x y -plane, the radius of the six congruent circles be 1 , and the ellipse be a 2 x 2 + b 2 y 2 = 1 . Then the four sides of the square are x = ± a and y = ± a .
As the figure is symmetrical about the origin, we can just consider the first quadrant. Let the tangent point of the two unit circles and the ellipse in the first quadrant be P ( x 0 , y 0 ) . Then the lower unit circle centered along the x -axis is ( x − 1 ) 2 + y 2 = 1 . Let the center of the upper circle be Q ( x 1 , y 1 ) , then x 1 = 1 + 2 ( x 0 − 1 ) = 2 x 0 − 1 . But x 1 = a − 1 , Then we have 2 x 0 − 1 = a − 1 ⟹ x 0 = 2 a . From
⎩ ⎪ ⎨ ⎪ ⎧ a 2 x 0 2 + b 2 y 0 2 = 1 ( x 0 − 1 ) 2 + y 0 2 = 1 ⟹ y 0 = 2 3 b ⟹ 4 a 2 − a + 4 3 b 2 = 0 . . . ( 1 )
We note that at P ( x 0 , y 0 ) the gradients of the unit circle and the ellipse are equal.
⎩ ⎪ ⎨ ⎪ ⎧ a 2 x 2 + b 2 y 2 = 1 ( x − 1 ) 2 + y 2 = 1 ⟹ d x d y = − a 2 y b 2 x ⟹ d x d y = − y x − 1 ⟹ a 2 y 0 b 2 x 0 = y 0 x 0 − 1 ⟹ b 2 = a 2 − 2 a
And from ( 1 ) :
4 a 2 − a + 4 3 b 2 4 a 2 − a + 4 3 ( a 2 − 2 a ) a ( a − 2 5 ) ⟹ a = 0 = 0 = 0 = 2 5 Note that b 2 = a 2 − 2 a Since a > 0
Then b = 2 5 , x 0 = 4 5 , y 0 = 4 1 5 , x 1 = 2 3 , and y 1 = 2 y 0 = 2 1 5 .
Let the center of the right dash circle be S ( x 2 , 0 ) and its radius r . Then x 2 + a = x 2 + 2 5 = r and
( x 1 − x 2 ) 2 + y 1 2 + 1 ( 2 3 − r + 2 5 ) 2 + 4 1 5 r 2 − 8 r + 1 6 + 4 1 5 ⟹ r = r = r − 1 = r 2 − 2 r + 1 = 8 2 5 Squaring both sides
Let the radius of the violet circle be r 1 . Then we have:
x 2 + r − a r − 2 5 + r − 2 5 4 2 5 − 5 ⟹ r 1 = 2 r 1 = 2 r 1 = 2 r 1 = 8 5
Therefore R = r r 1 = 2 5 5 = 5 1 ⟹ ⌊ 1 0 5 R ⌋ = 2 0 0 0 0
Wow! That is almost about the same solution (except that it is more geometric) I came up! Well done!
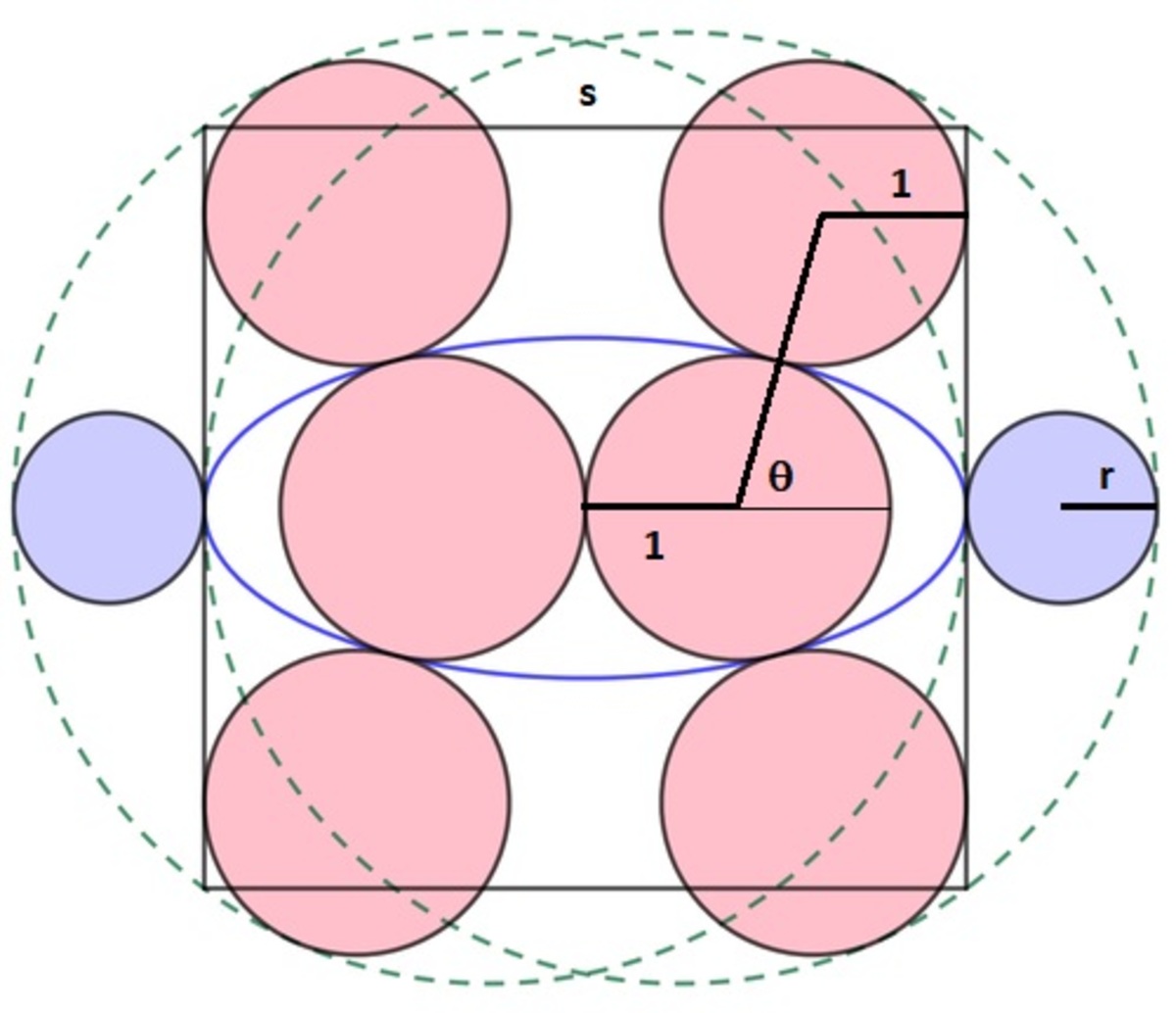
Let the radius of the pink circles be 1 , and side length of the square by s , and the let the angle that the line segment joining the centers of the right central pink circle and the upper right pink circle, makes with the horizontal direction be θ . Note that the ellipse has a semi-major axis of 2 s , and let's call its semi-minor axis b . Finally, let the eccentric angle of the point of tangency between the two aforementioned pink circles be t , then we can write the following relations between these four variables, which are s , θ , t , b :
Firstly, taking the horizontal distances along the path indicated in the figure above, we get,
2 + 2 cos θ = s / 2 ( 1 )
Next, the tangency point satisfies:
T = ( 1 + cos θ , sin θ ) = ( 2 1 s cos t , b sin t )
so that,
1 + cos θ = 2 1 cos t ( 2 )
and
sin θ = b sin t ( 3 )
and finally, since the parametric equation of the ellipse is ( 2 1 cos t , b sin t ) , then its tangent vector is along ( − 2 1 sin t , b cos t )
and this tangent vector is perpendicular to the line joining the two centers of the two pink circles whose unit vector is ( cos θ , sin θ ) , therefore,
− 2 1 s cos θ sin t + b sin θ cos t = 0 ( 4 )
Applying the Newton-Raphson method, we define our vector function to be
f = ⎣ ⎢ ⎢ ⎡ f 1 f 2 f 3 f 4 ⎦ ⎥ ⎥ ⎤
where
f 1 = 2 + 2 cos θ − s / 2 ( 5 )
f 2 = 1 + cos θ − 2 1 cos t ( 6 )
f 3 = sin θ − b sin t ( 7 )
f 4 = − 2 1 s cos θ sin t + b sin θ cos t ( 8 )
Let our variable vector be
x = ⎣ ⎢ ⎢ ⎡ s θ t b ⎦ ⎥ ⎥ ⎤ ( 9 )
Then according to the Newton-Raphson iteration, we start with an initial guess x 0 , and update our guess according to the following
recursive formula:
x k + 1 = x k − J − 1 f k ( 1 0 )
where the matrix J is the jacobian defined as follows:
J = [ J i j ] = [ ∂ x j ∂ f i ]
Implementing this method, led to the solution in just 4 iterations. The solution is
x = ⎣ ⎢ ⎢ ⎡ 5 1 . 3 1 8 1 1 6 0 7 1 1 . 0 4 7 1 9 7 5 5 1 1 . 1 1 8 0 3 3 9 8 9 ⎦ ⎥ ⎥ ⎤
Now, we need to find R the radius of the big circles, and r the radius of the small circles. Passing a line through the center of the upper right pink circle, making an angle ϕ with the horizontal direction, and noting that the y-coordinate of the center of this circle is y = 2 sin θ , then we want to find ϕ such that
R = 1 + y csc ϕ = s − 1 − y cot ϕ
Multiplying through by sin ϕ ,
sin ϕ + y = sin ϕ ( s − 1 ) − y cos ϕ
whose solution is ϕ = 1 . 1 4 6 4 0 6 6 1 7 , from which it follows that R = 3 . 1 2 5 = 8 2 5
Finally, the radius of the small circle is r = 2 1 ( 2 R − s ) = 0 . 6 2 5 = 8 5
Hence, R r = 2 5 5 = 5 1 = 0 . 2
And this makes the answer ⌊ 1 0 5 ( 0 . 2 ) ⌋ = 2 0 0 0 0
The ellipse and the pink circles are just red herrings. Leave them out and the thing is very simple. That can be done once you realize that fixing the square fixes everything else. Leave the left dashed circle and the left violet circle away as well.
Let the square have vertices ( 1 , 1 ) , ( − 1 , 1 ) , ( − 1 , − 1 ) , ( 1 , − 1 ) .
Then the dashed circle must be centred at ( x , 0 ) , such that its distance to (-1,0) and (1,1) is equal. We find x = 4 1 and the radius of the dotted circle equals R = 4 5 .
The rightmost point of both circles is at x + R = 2 3 .
The radius of the small circle is r = 2 1 ( 2 3 − 1 ) = 4 1 .
The ratio of the radii equals 5 / 4 1 / 4 = 0 . 2 and the answer is ⌊ 0 . 2 × 1 0 5 ⌋ = 2 0 0 0 0 .