Paddling, paddling, paddling!
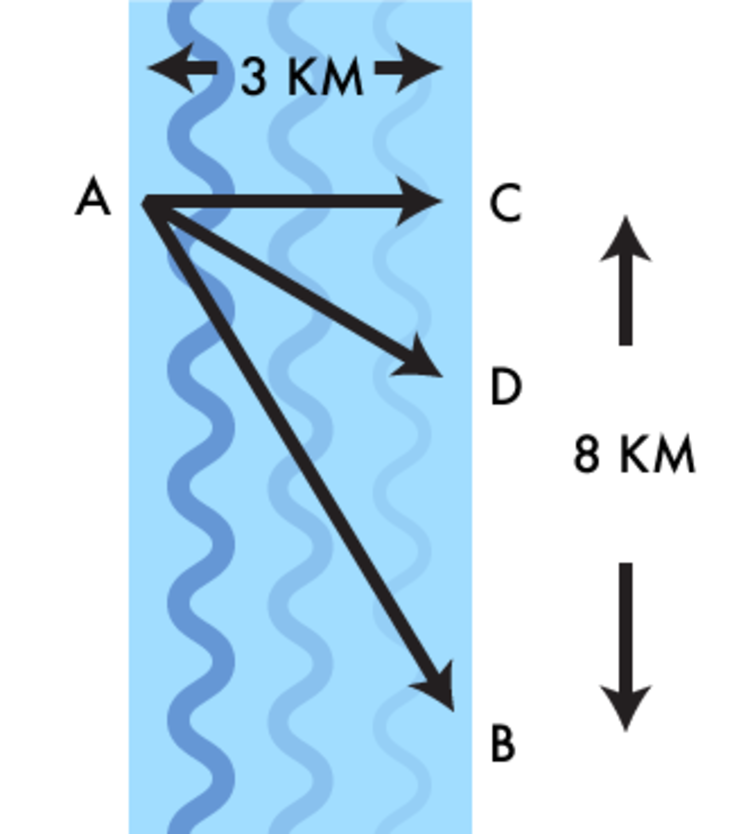A man paddling his boat from point A on riverside 3 km straight. He wants to reach point B which is 8 km more downstream in the opposite side(see Figure). He can paddle boat and run to C to B, or he could pedaling directly to B, or he could row to some point D between C and B and then run to B. If he can row the boat with a speed of 6 km/hr and run with a speed of 8 km/hr, where should he land in order to reach B as soon as possible? The Answer unit is expressed in km :)
The answer is 3.4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Let CD = x. So AD = sqrt(9+x^2) and DB = 8-x. The time taken from A to B is
f(x) = AD/6+DB/8 = sqrt(9+x^2)/6+(8-x)/8. Solving for critical points,
f'(x) = 0,
x/[6*sqrt(9+x^2)]-1/8 = 0,
8x = 6*sqrt(9+x^2),
64x^2 = 36*9+36x^2,
x^2 = 36*9/28 = 81/7,
x = 3.4017 km.
Since f'(0) = -1/8 < 0 and f'(4) = 1/120 > 0, so f has a global minimum at CD = x = 3.4017 km.