Paint it red

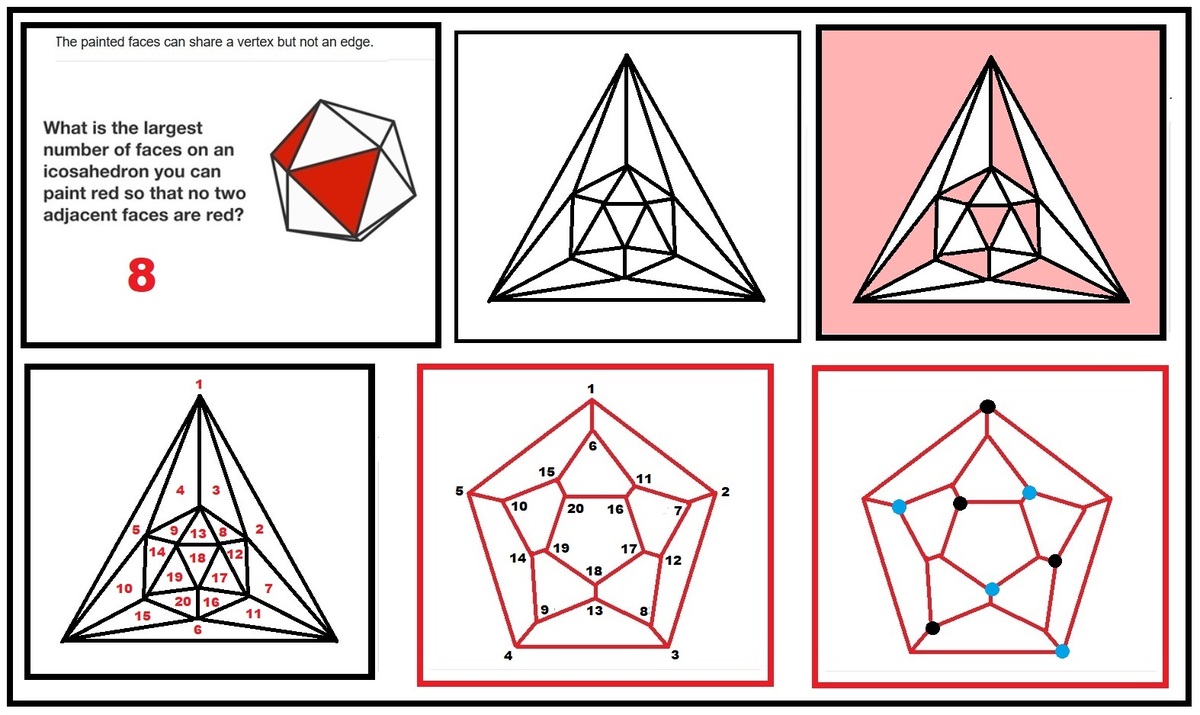
Each vertex in a icosahedron is surrounded by $5$ triangular faces, and with the given restrictions at most $2$ of those $5$ faces can be painted red, as shown below.

Since there are $12$ vertices in the icosahedron, with at most $2$ painted triangular faces around each vertex, and each triangle has $3$ vertices, the most possible painted faces in an icosahedron with the given restrictions would be $\frac{12 \cdot 2}{3} = \boxed{8}$ , and one possible way to do this is shown below.

The icosahedron is the dual of the dodecahedron in which the faces of the icosahedron are the vertices of the dodecahedron and the faces of one are the edges of the other. Adjacent faces in one become connected edges in the dual. Viewed this way, the task is to find a maximal subset of unconnected vertices in the dodecahedron that corresponds to a maximal set of non-adjacent faces of the dual figure. (Bear in mind that the exterior of the icosahedron figure represents one face of a three-dimensional figure.)

The strategy employed was, paradoxically maximizing not minimizing the faces affected, to select four vertices of the dodecahedron having no face in common ( marked with black dots in the diagram). This is the minimum and maximum possible since each vertex affects 3 faces (of the dodecahedron) and since they have no face in common, at least four are required to get 3x4 = 12 faces, and since each affects 3 faces (for a total of 12) every other vertex must have a face in common with at least one of them. Eliminating all the vertices that are connected to these four leaves another four (marked in blue in the diagram) for a total of 8 . The vertices are then mapped back into the icosahedron as shown to color 8 non-adjacent faces.