Paint the horn
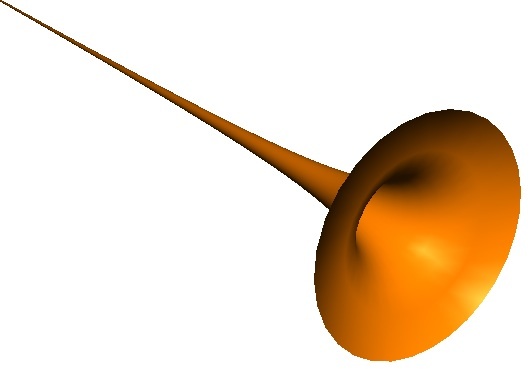 A hypothetical horn is constructed, which is described by the parameters
as
A hypothetical horn is constructed, which is described by the parameters
as
If it is required to paint the interior of the horn. If 100 square units of the interior surface can be covered using one cubic unit of paint, of the available options what is the minimum number of cubic units of paint that would ensure that the entire interior of the horn is covered in paint.
This problem is not original.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The horn is the surface of revolution formed by rotating z = − r 1 about the z axis.
This gives the volume and area of the horn as
V = a → ∞ lim π ∫ 1 a r 2 1 d r = a → ∞ lim π ( 1 − a 1 ) = π
and
A = a → ∞ lim r 1 1 + d r d ( 1 / r ) d r > a → ∞ lim r 1 d r = ∞ .
Hence, the horn has an infinite surface area, but a finite volume of π .
Thus, π cubic units of paint can ensure that the entire interior surface is covered in paint. Among the choices, the least valid number is 2 3