62 Colors

Probability Level 3

This is the Great Rhombicosidodecahedron (one of the Archimedean Solids):

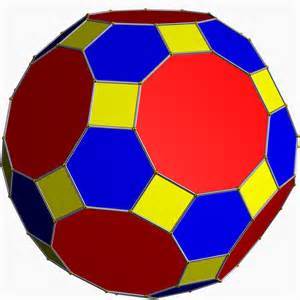
In this picture it is colored using $3$ different colors.

However, suppose you have $62$ different colors, and you wish to paint each of its $62$ faces in a different color.

Let $\dfrac{a}{b}$ be the ratio of the number of unique ways to paint this solid divided by the total number of ways this solid can be painted, where $a$ and $b$ are coprime positive integers.

What is $a+b$ ?

Note : Unique implies that for two coloring combinations $A$ and $B$ , you can't pick up $A$ and reorient it to make it look exactly like $B$ .

Image credit: commons.wikimedia.org

The answer is 61.

1 solution

Geoff Pilling
Sep 15, 2016

The divisor of this ratio is equivalent to saying "How many different ways can you orient this solid and have it look the same?", or the redundancy of taking all the combinations of coloring the solid vs all of the different ways ("different" as defined in the problem).

To orient this solid, lets choose one of the regular decagons (red in the picture) as a base. There are $12$ of them, so you have $12$ choices. For each choice, there are $5$ possible rotations each with yield an equivalent view of the solid.

Therefore there are $12 \times 5 = 60$ equivalent ways to orient this solid.

So, $\frac{a}{b} = \frac{1}{60}$

$1+60=\boxed{61}$

Geoff, the Great Rhombicosidodecahedron has 62 faces, not 120. Its dual has 120 faces, which is actually what the Brilliant Logo is based on, a Catalan solid. Change the wording from 120 to 62, otherwise your problem is fine.

Michael Mendrin - 4 years, 9 months ago

Ah, right you are... I was thinking about vertices... Thanks for the observation... I've updated the problem! (Good thing the 62 cancels out!)

Geoff Pilling - 4 years, 9 months ago

Actually, in solving this problem, I did examine the ways this polyhedron could be rotated from one vertex to another, which split all such rotations into 2 equal but separate groups---that is, 120 = 60 + 60. And so the answer follows from that.

The fact that all 120 vertices divide into 2 classes of 60 each corresponds to the 120 faces of the dual Disdyakis triacontahedron that divide into just 2 kinds, one right and one left.

Michael Mendrin - 4 years, 9 months ago

62 Colors

Image credit: commons.wikimedia.org

The answer is 61.

1 solution

0 pending reports