Painting New Construction
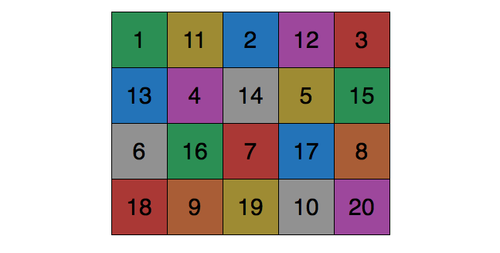The construction foreman at Bayview is overseeing 20 houses arranged in 4 rows of 5. It would take 1 full day to paint each house, and he has 20 days to paint all the houses. To avoid a buildup of toxic paint fumes, he wants to maximize the minimum number of days between which 2 adjacent (vertically, horizontally or diagonally) houses have been painted. What is the maximum number of days?
For example, if the above diagram indicates the day in which those houses were painted, then the minimum number of days in which 2 adjacent houses were painted is 2. The houses numbered 4 and 6 and were painted 2 days apart.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
It is easy to find a construction where the minimum difference is 4 days. For example,
How do we show that it is the maximum?
Suppose not, that there exists a construction where the minimum is more than 5. Consider the day that the house in position ∗ gets painted. Then,we see that we can spend at most 4 days painting the houses marked with 1 , after which the 5th day must be spent painting a house marked with 0 . Notice that if we refrain for 4 days, then the house marked with 1 a must be painted during those 4 days. However, since 1 a is unique, this means that the house marked ∗ either doesn't have 4 days before it where houses are painted, or doesn't have 4 days after it when houses are painted. Hence, it must be painted before the 4th day, or after the 16th day.
Repeat the analysis with the house marked with 1 ∗ , and we see that the same holds. Show that this means that both houses are painted either "before the 4th day" or "after the 16th day" (scenarios are symmetric). Show that this leads to a contradiction.