Painting Squares
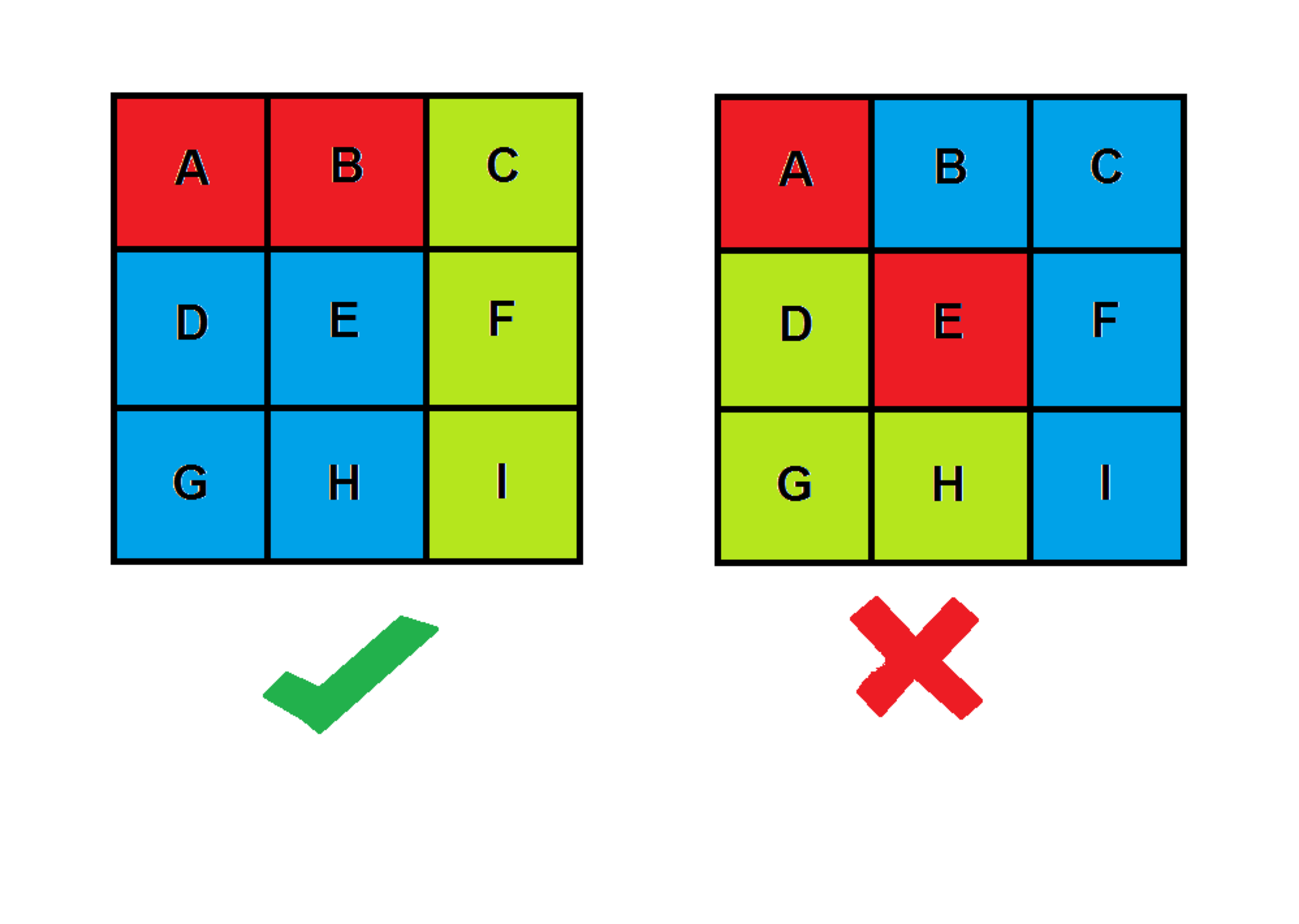
You have a squares designated with alphabets to distinctly. You would like to color 2 squares red, 3 green, and 4 blue such that each same colored squares are connected together. For example, the figure on the above left suits the constraint while the one above right does not because the red squares do not have any edge in common.
How many ways are there for you to paint these squares?
The answer is 48.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
By coloring the blue squares as a bigger square, 4 combinations can be generated from rotating around the center, as shown above.
Then there will 2 combinations for each of the 4 variations, leading to total of 8 outcomes.
Similar to the first case, 8 more outcomes are created by rotation.
For L-shaped figure in the center, there is only one way to color red and green though by reflection, the number of outcomes is doubled for 4 rotated ones, totally of 8 .
Finally, for the L-shape in the far side, there are 3 ways to color the other two colors, 4 rotations, and 2 reflections. Thus, it will add up to 2 × 3 × 4 = 2 4 ways.
As a result, there are 4 8 ways to color the squares.