Pangs, Pings and Pongs
True or False?
All pangs are pings.
Some pings are pongs.
Therefore, some pangs are pongs.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
14 solutions
Thanks! Visual representation of the Venn diagram in this form is certainly helpful!
Log in to reply
True, some pangs are pongs
The 'trick ' is in the very first statement: "All pangs are pings." Once I tried to extract factors which tricks the mind and note down them. I thought I could use them in problem posing.
This problems uses a classic one in which the very first data is easy to misunderstand. Any data which is difficult to understand isn't as tricky as the one which is easy to misunderstand .
This may come handy when we are in a mood to play around and irritate our buddies :D
I would like to know more about the 'Hypothesis'.
"All" is a subset of "Some". The question is flawed.
It says that ALL pangs are PINGS. Then it says SOME PINGS are pongs. Can someone explain why this means that "some pangs are pongs" is incorrect? I am pretty sure the question is flawed.
Log in to reply
All people are mammals and some mammals have tails thus some people have tails. True or false 😊
Log in to reply
Well, some people DO have tails... malformation but still.
I see your point
Well,this is a very common problem that is asked in NTSE every yr and almost asked in every logical reasoning test and IQ test.I learnt it using doing venn diagrams.They actually come in NTSE like assertion reason.They give the two starting statements as your problem and then 2 reasons or conclusions and we have to find which is true and why.
I chose "False, none of the pangs can be pongs" because I thought it fit the most:
"False, there might not be a pang that is a pong" just says something about the nonexistence about a single pang-that-is-a-pong. However, "False, none of the pangs can be pongs" has the word "can" in it.
All pangs are pings. Some pings are pongs. Therefore, some pangs are pongs.
Does the first statement make the words ping and pang interchangeable, thus making Some Pangs are pongs true
Log in to reply
All pongs are pings doesn't mean that pongs and pings are the same thing. If an element is pong then it is a ping. But if an element is a ping it could be not a pong. The difficulty here comes from the way the phrase is written.
All squares are rectangles. Is the perfect example of how the first statement is tricky and does not make ping and pang interchangeable.
One of the option says there are SOME pangs that are pongs. It does not mean all. So these two options are the same.
This question is flawed. It is true that not all pangs are pongs, but that would mean that some are.
Easy to solve with this diagram
Yes, but some pangs could possibly be pongs. It seems like a badly worded question, making the meaning unclear.
Why do you infer that there are Pings that are not Pangs? Either you cannot infer the opposite (that all Ping are Pangs) ... so I believe that "True, some pangs are pongs" and "False, there might not be a pang that is a pong" are correct, depending how is your belief about the information that is not given.
Without saying that not all pings are pangs, we could also assume that ping=pang. Which is not the same.
I think without the the statement "some pings are not pangs." Or some facsimile of the statement one can't determine that pings exist outside of pangs. Therefore choice A is not necessarily true.
That's exactly how I did it as well.
Well, I don't know, but I thought of it this way: pang=x, ping=y, pong=z. if x=y, and x are some of z, would that mean that y are also some of z since x and y are just equal (or let's say the same)? Well, I think it depends on the perception of a person. However, if we picture the three as some things other than leaving them unidentified and vague, then the conclusion might change. Like birds! If all chicken are birds, and some birds are penguins, does that mean that all chicken are penguins? In that case, we could say that the third statement is false.
I'm sorry but I think the English is confusing. If the option was "There might be a pang that is a pong" or "There might be a pang that is not a pong", I would agree. But "There might NOT be a pang that is a pong" is not correct with the given propositions. One example: - all Jaguars are cars - some cars are blue - therefore, some jaguars are blue. We can't say the the conclusion is true, but we can't also say that it is false. We can't say that "there might not be a blue Jaguar".
Actually it is true, some pangs are pongs for this reason: All pangs are pings. Some pings are pongs Some pangs are pongs, true or false? It is true, because the requirement for true is that there exists at least one pang that is a pong, and, shown by your Venn diagram, there are some that exist. I would highly advise fixing this, because it is not false. At all.
Log in to reply
The pings that are pongs need not be pangs.
Drawing the conclusion is not valid, because we do not have enough evidence to conclude that it must be true.
Look at it like this all squares are rectangles but not all rectangles are squares. We are told all pangs are pings but we are not told or could we know if all pings are pangs thus making it possible that some pings are not pangs.
"All pangs are pings." Alright, straightforward, but this does not imply the converse: all pings are not necessarily pangs.
"Some pings are pongs." Alright, but which pings exactly?
"Some pangs are pongs." Wait a minute, that doesn't have to be true! All the pongs could be pings that are not pangs!
This was basically what ran through my head when I was solving this problem. I realize it's not formal at all, but more of intuitive reasoning, which seems like what your friend wants to investigate.
I'm curious to hear his hypothesis and whether or not this experiment supported it!
Thanks for your solution!
Log in to reply
Here is my solution to finding the answer to be true; if all pangs (dogs) are pings (animals) and some pings (animals ) are pongs (black) then couldn't some pangs (dogs) be pong (black)
Log in to reply
This may be true, but then some of the dogs may not be black; they may be white or brown. So some pangs (dogs) may not be pongs (black).
Thank you SO much, this clears all my confusions
All cows eat grass. Some that eat grass are sheep. Therefore some cows are sheep?
Thanks for your solution!
False analogy upon pre existing knowledge of animals. Stephen King makes popular books. Some popular books are movies Therefore, Some of his books are movies.
Log in to reply
Liam's analogy only shows that the conclusion could be true in certain cases. It does not show that the conclusion must be true in all cases, which is what this problem asks.
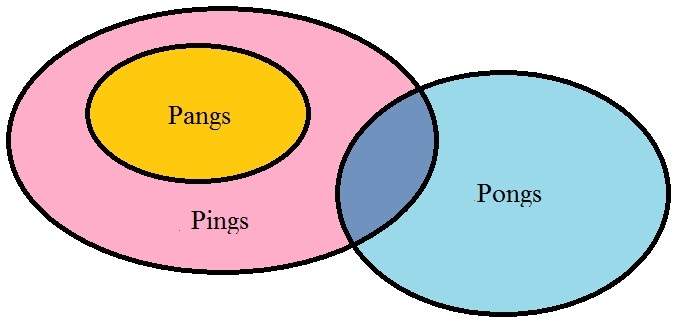
False, there might not be a pang that is a pong
I just substituted pangs for humans, pings for apes, and pongs for gorillas.
All humans are apes. Some apes are gorillas. But no humans are gorillas, therefore the statement is false.
I used the following example:
All humans are animals. Some animals are zebras. Therefore some humans are zebras.
After this example, I realized that the answer HAD to be False. The second part was a bit more complex. We know that humans are definitely NOT zebras, but the example limits the set. Given another set, there is a possibility that a "human" could be a "zebra", maybe in a parallel universe or something!
In first order logic, an argument is valid if the premise implying the conclusion is a tautology. However, this is not a tautology, making the argument False.
To show that the argument is not a tautology, it suffices to construct one model where the conclusion is false, the premises being true.
We also need to show that the argument's validity contingent. To show this, we need to construct a model where both the premises and the conclusion are true.
I will complete these proofs more formally when I come back from school.
Using Aristotelian Logic,
All PANGS are PINGS → SaP Statement , + Some PINGS are PONGS → SiP Statement , +
Asserted conclusion: Some PANGS are PONGS → SiP Statement , +
Required Conditions
- (1) If all the statements are + ve, then the conclusion must be positive ✓
- (2) Middle term must be underlined ×
- (3) Any term distributed in the conclusion must be distributed in any of the statements ✓
So the conclusion given in the question is wrong. Since Condition (2) is not satisfied in any case, we cannot say to certain what is true. Hence the answer.
Moderator note:
Good approach used here, that is different from the rest.
In an infinite time always will be true because always is there a little chance to be. The statement of pings, pongs, pungs or whatever is too abstract to infer only a limited number of data.
"All pangs are pings" alright pretty straightforward "Some pings are pongs" alright so not all pangs ar pongs
Log in to reply
Sorry i pressed the wrong button but I'll finish it here "Therefore, Some pangs are pongs" Answer "false because there might be a pang that's not a pong" Those that you are referring to, pangs that aren't pongs, aren't part of the 'some' stated in the third statement. Therefore, you may be correct, but you have the wrong reason, which is a key thing to have
According to me, the syllogism is as below..
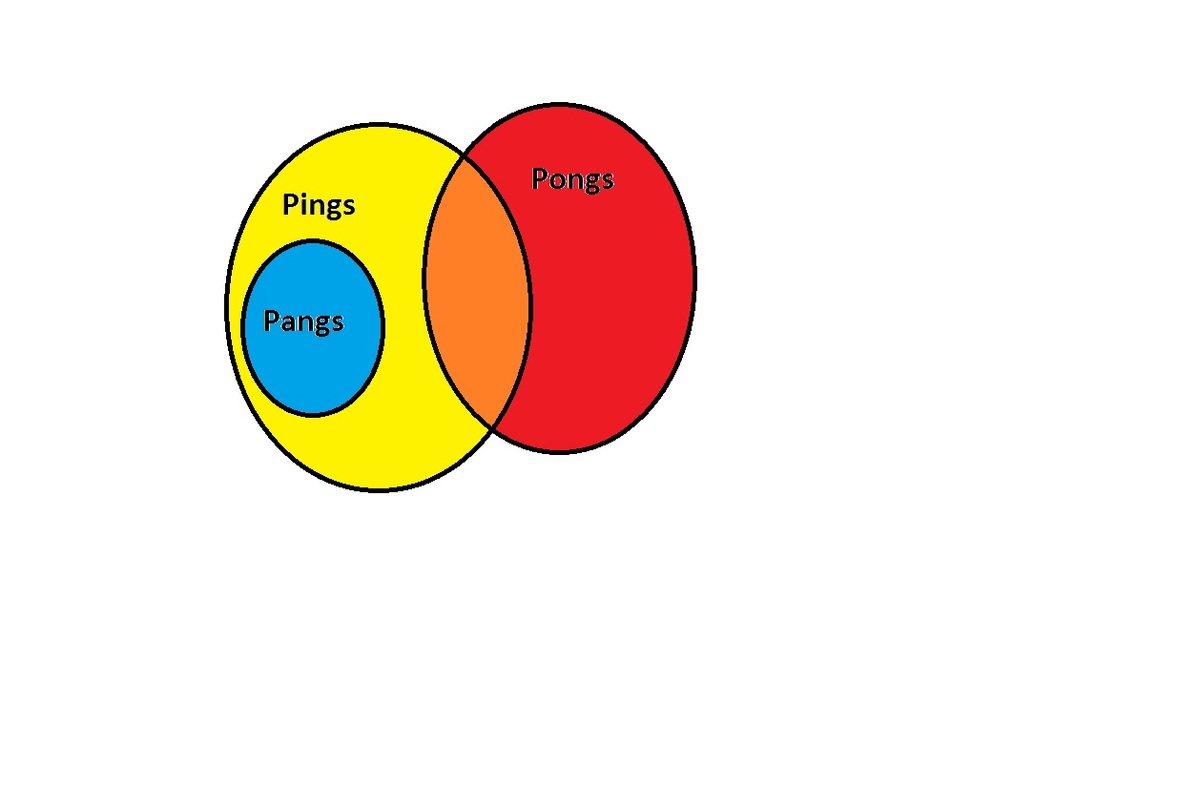
The case of any pang being pong should not arise as it has not been specified by the question.
(I'm new here, and since I do not know Latex, I shall type what I thought) Let P be the set of all Pangs, P1 be the set of all Pings and P2 be the set of all Pongs. Clearly, P is strictly a subset of P1. Some elements of P1 can be expressed as an intersection of P1 and P2. Now, these elements may or may not belong to P. Therefore, there might not be a Pang that is a Pong.
"All pangs are pings"
Assume pings is a set of 4 numbers, 1 of which is a pang.
"Some pings are pings"
Assume half of the pings are pongs. There are ways to chose 2 elements of the set Ping so that none or 1 is a pang.
Thus only some (if any) are pangs.
Btw, I'm very interested as to your friends hypothesis on how different people solve this problem. Sounds like a very cool thing to study.
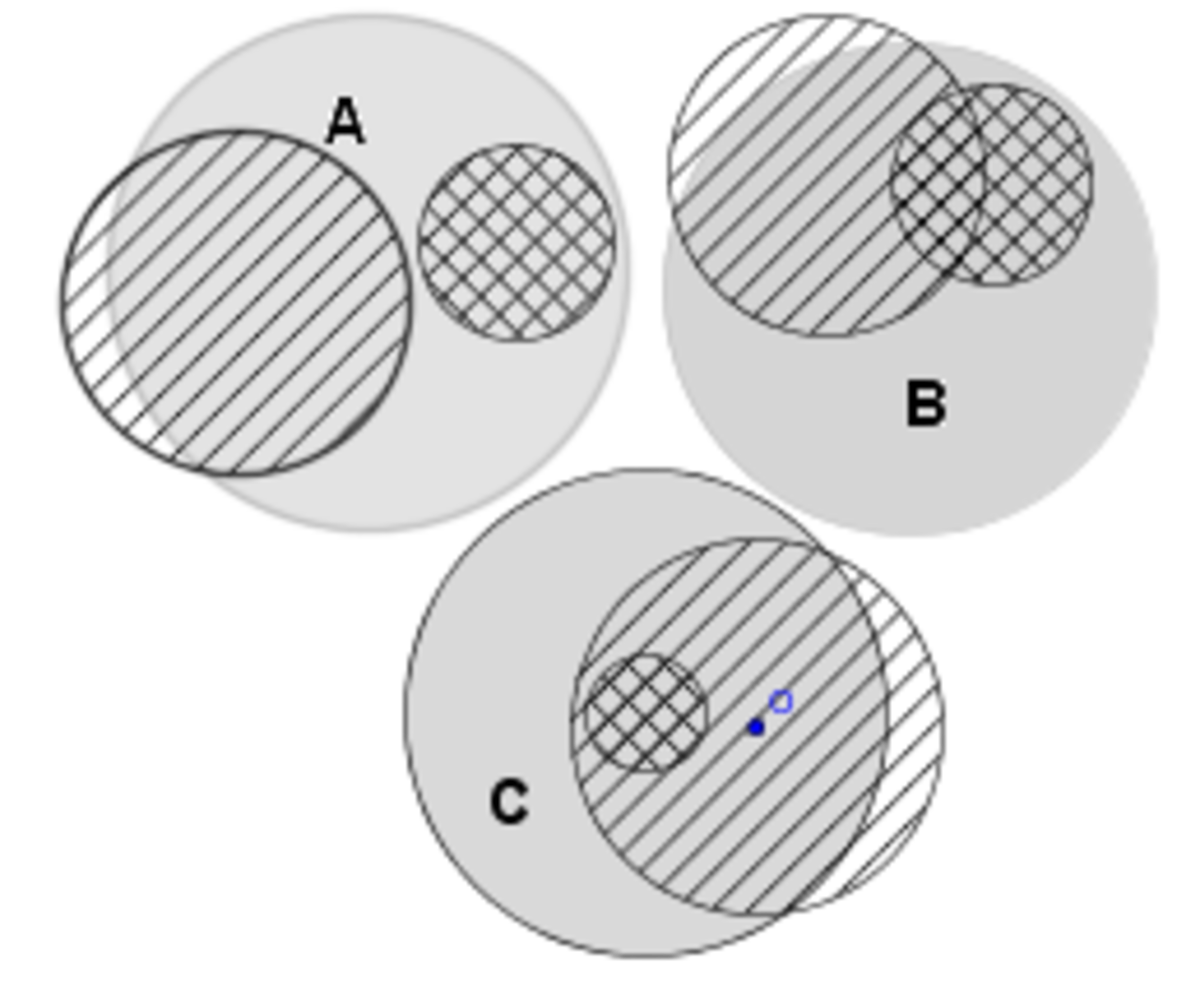 Ping large O
Ping large O
Pang Hatched O
Pong Cross Hatched
Hence The statement is true only for Case B
This is a pretty simple logic problem, So we have three groups, a smaller group that is pangs, all of them are a sub-sect of pings, so then we have the third group pongs, some of the ping group overlap the pong group, but we don't have enough information to determine if any of the pang grouping is actually part of the pong grouping, while there MAY be some that are we can't say for sure, where the answer "true, some pangs are pongs" may be true we don't know that for certain, HOWEVER, the "False, there might not be a pang that is a pong." we don't know some might be but there MIGHT NOT be, so this statement is the best solution it does not say that none of them are, it just says there might not be any pangs that are pongs, which is true, without further data we can not determine if any pangs are pongs.
The shortest version to try to explain this is, a hypothetical we have 15 people as represented in this line
| --------------- |
Now we know that the smaller group, Pangs are all inside this group so let's make a division, say 5 of them
|----- // ---------- |
Now let's make cases for the third group, some of group 2 are part of group three. The members that are part of both groups signified by x.
|----- // --- // xxx // ---- |
Case two:
| ---xx // --- // xxx // --- |
either case could be accurate so in this vein we don't know for certain so we should take the answer that indicates that while it may not be true, the key here is in that less than solid phrasing, Might not, does mean can not, it does not mean that any are, it simply states that they may not be, which also means some may possibly be. Might is non-definitive, and without more information we can not give a definitive answer.
Here are three distinct solutions that come to mind.
Solution 1
These are two of the options: "True, some pangs are pongs", and "False, there might not be a pang that is a pong". The latter can be translated to "it is false that some pangs are pongs", so these two are complementary. Thus one of them must be true, reducing our options to two. We can then use Venn diagram or anything of the sort to show that the answer is not true, so the answer has to be False, there might not be a pang that is a pong .
Solution 2
We solve this with two constructions.
- Suppose there is no pang at all. This causes the first premise to be true vacuously, and it's easy to make the second premise true (there is exactly one ping, which is itself a pong). However, the conclusion is clearly false; there is no pang at all, how can there be a pang that is also a pong? This makes the True answer incorrect.
- Suppose there are two pangs, both pings. One pang is also a pong; the other isn't. This makes two of the False answers incorrect: "no pang is pong" is made incorrect, and "all pang is pong" is also made incorrect.
This leaves the sole option that has the uncertainty: False, there might not be a pang that is a pong .
Solution 3
Three of the four options actually assert syllogisms . The true option asserts the syllogism IAI-1; the "no pang is pong" option asserts the syllogism IAE-1; the "all pang is pong" option asserts the syllogism IAA-1. The last option asserts the negation of IAI-1. We can see that none of the three syllogisms are valid (there are only 24 valid syllogisms; just find some list of them), so the correct option is the one asserting the negation of IAI-1: False, there might not be a pang that is a pong .
Thanks for your solution!
- Transitive law-If A is equal to B and B is equal to C, then A is equal to C
- set A is a subset of set B and set C is the intersection of A and B. Therefore some elements of A are also in set C
From the first statement we can draw the following venn diagram: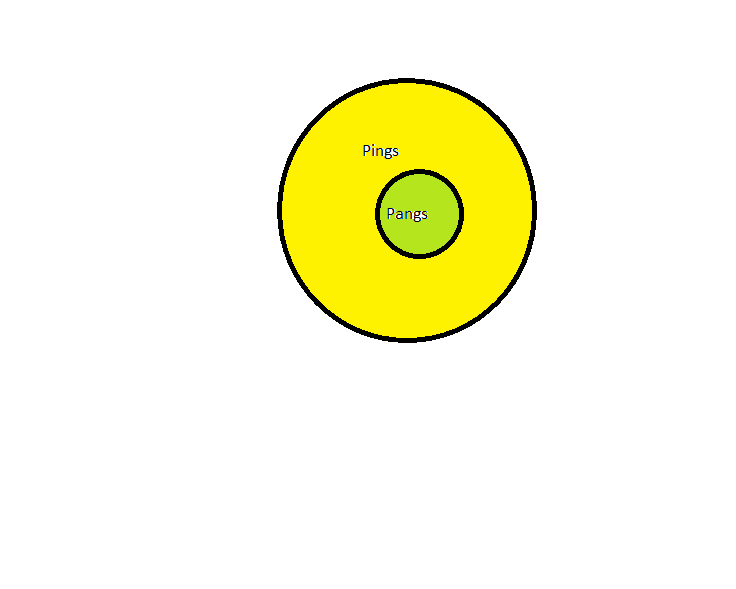
From second statement two cases arises which are shown as: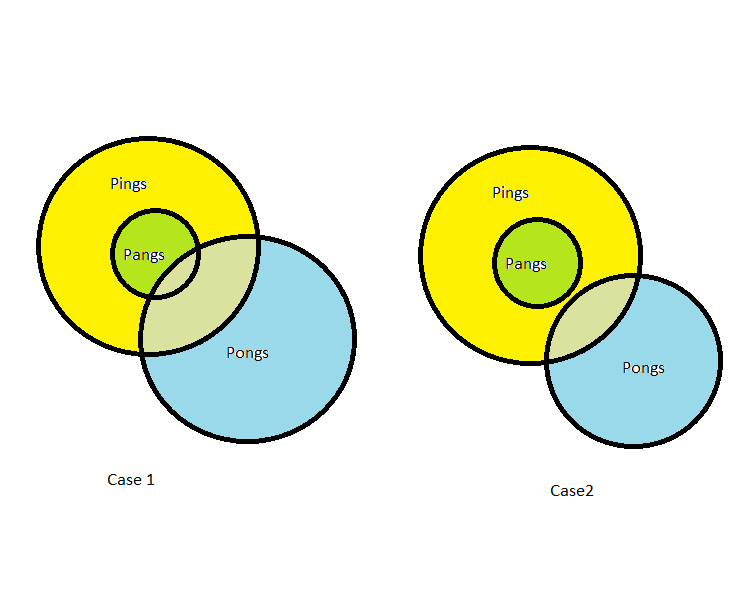
Hence we are not sure that which is true as nothing is said .Hence the correct option is " False, there might not be a pang that is a pong"