Paper
A B C D and A ′ B C ′ D are both rectangles with side lengths A D = A ′ D = 2 , A B = A ′ B = 6 . Find the area of shaded region (to 2 decimal places).
The answer is 6.67.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Why the intersection of the rectangles is a rhombus
Log in to reply
From symmetry. Both rectangles are the same, so D H = H B , and equal to the other side as well, as the rectangles are themselves symmetrical.
How do you know the scale factor of ∆DBC to ∆DHG is 1/3?
Log in to reply
Sorry I misread the solution
how DBC is similar to DHG ?
Log in to reply
They are both right triangles sharing the angle D B C .
Let
D
C
and
A
′
B
intersect at
H
.
Let
A
B
intersect
C
′
D
at
I
.
Then the figure is symmetric about the line I H . Hence, we have D H = H B . Set this length to be x .
Applying Pythagoras theorem on triangle B H C , we have B C 2 + B H 2 = B H 2 , or that 2 2 + ( 6 − x ) 2 = x 2 . Expanding and simplifying, we get 4 + 3 6 − 1 2 x + x 2 = x 2 , or that x = 1 2 4 0 = 3 1 0 8 .
Hence, the blue area, which can be calculated as base DH * height BC, is 2 × 3 1 0 ≈ 6 . 6 7 .
Please rephrase the Pythagorean part! BH squared =BC squared + CH squared!!
2 × 3 8 is equal to 3 1 6 ≃ 5 . 3 3 ... You made a mistake by saying that 1 2 4 0 = 3 8 . It is actually 3 1 0 , you know!
Log in to reply
Thanks! I fixed the typo.
how DH = HB ?
Log in to reply
Let AB intersect C'D at I.
Then the figure is symmetric about the line IH.
Let me add that in.
As @Calvin Lin said, we can see a Symmetry in the image. When we analyse the geometric relations of the problem, we can see that the shaded figure is a rhombus, due to the congruence of the triangles inside the shaded quadrilateral.
We can see an angle θ=DGH (where H is the centre of the diagonals of the quadrilateral), that is half of the angle DHA' - since DB is the diagonal of both rectangles - and so we can ensure that the angle θ really is the smallest of the other triangles (see wiki https://brilliant.org/wiki/sat-parallel-lines/).
This pattern is applied to the other sharp angle, and since all the angles in the rectangles are equal to 90°, we have proved that the triangles mentioned are congruent, and so, DH=HB!
Forgetting the rhombus, I took your triangle BHC and used Pythagoras in much the same way to find HC = 2.66667. At that point, it was easy to multiply that by 2 to find the total unshaded area of ABCD, which is then subtracted from 12 to find the shaded area.
This solution needs access to trigonometric tables. However, in case if we use Tan 2x= 2 Tan x / (1-(Tan x)^2) we need not rely on trigonometric tables.
x is much easier to arrive at. Assuming that x^2 + 4^2 = y^2 where y is the hypotenuse in the triangle A1 then assuming that y = x - 6 since we know that DC = 6 then since using Marta's diagram FH = HC = x then y = 6 - x since FB (Marta) actually equals A'C = 6 and A'H (mixing the diagrams) = 6 - x so we sub through, and x^2 + 4 = (6 - x)^2 which is x^2 + 4 = 36 - 12x - x^2 which is actually 12x = 32 which is 32/12 which is 8/3
Note that all the triangles around the shaded region are congruent. This can be easily proved using AAS congruency as all triangles have AD=BC=A'D=BC'=2 and one angle is 90 degrees while the other can be shown equal by some angle chasing.
Let us say that AB intersect C'D at X and let us call AX = x and thus XB = 6-x . Now as ADX is congruent to C'BX we get C'X = AX = x . Now in triangle C'BX, by Pythagoras' theorem we have
C'B^2 + C'X^2 = XB^2
or 2^2 + x ^2 = (6- x )^2
which solves to x = 8/3
The triangles' area become = 1/2 * 2 * 8/3 = 8/3
Now the shaded region's area is = area of rectangle - 2 * area of triangle
= 2 * 6 - 2 *8/3
=12 - 16/3
= 20/3
=6.667 or 6.67
When you found x, it's faster to use the fact that the area of the rhombus is base x height = 2x
Log in to reply
Yes, agree. The crux was to find x, after that many ways to find area.
This was my exact strategic, except that we already knew the height of the triangle, as has been previously mentioned.
If the side length of the rhombus is x, then we see right-angle triangles with sides 2, x, and (6-x).
Pythagoras:
x ² = 2 ² + ( 6 − x ) ²
x ² = 4 0 − 1 2 x + x ²
x = 4 0 / 1 2 = 1 0 / 3
The area of a parallellogram is base × perpendicular height
= 2 × 1 0 / 3 = 6 ⅔ = 6 . 6 7
That is the easiest way to solve problem. Nice job!!
Exactly what I did! I was about to type it up and you had beaten me to it.
That's also what I did! 8 prefer this solution as in my opinion it is much easier to understand than the other ones.
I think this is the most elegant solution. No trig, and once you recognize that the hypotenuse of the rt triangle is 6-x, the solution falls in your lap...the x^2 cancels, so you don't even need the quadratic equation!
I will give a general solution for rectangles with width a and height b .
The shaded region is a parallelogram. To find its area, we must multiply the base b by the height y . The challenge is to find the value of y .
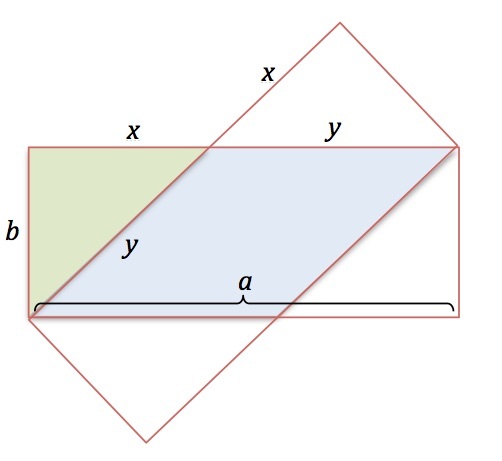
(In this drawing, the x s and y s are equal because of the obvious symmetry of the situation.)
On one hand, a = x + y . On the other hand, applying the Pythagorean Theorem to the green right triangle, y 2 = x 2 + b 2 . Substitution of x = a − y yields y 2 = ( a − y ) 2 + b 2 ∴ y 2 = a 2 − 2 a y + y 2 + b 2 ; 2 a y = a 2 + b 2 ; y = 2 a a 2 + b 2 . Thus the shaded area is A = b y = 2 a b ( a 2 + b 2 ) . In this case, a = 6 and b = 2 , so that A = 2 ⋅ 6 2 ( 6 2 + 2 2 ) = 6 1 ⋅ 4 0 = 3 2 0 ≈ 6 . 6 7 .
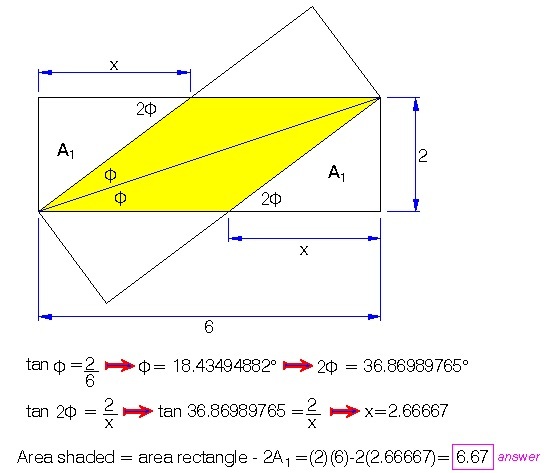

The diagonal D B = 6 2 + 2 2 = 2 1 0
△ D B C is similar to △ D H G therefore G D G H = 6 2 = 3 1
G H = 3 1 × G D = 3 1 × 2 D B = 3 1 0
A r e a = 2 1 0 × 3 1 0 = 3 2 0 = 6 . 6 6 7