Paper Folding 1
A square paper of side length 1 is folded along the segment that connects the upper right corner and the midpoint of the left edge, as shown.
What is the vertical distance between the base edge and the red dot at the corner flipped over?
The answer is 0.2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
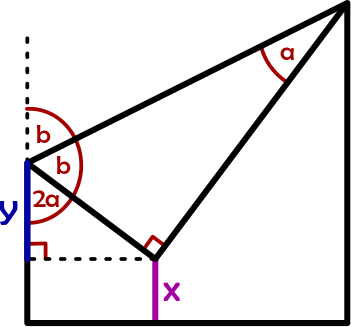 Consider the picture shown, the folded triangle has sides
2
1
and
1
and hypotenuse
2
5
, now from the small right triangle we have
cos
(
2
a
)
=
1
/
2
y
hence
x
=
2
1
−
y
=
2
1
−
2
1
cos
(
2
a
)
=
2
1
−
2
1
(
cos
2
a
−
sin
2
a
)
replacing we get
x
=
2
1
−
2
1
(
(
5
2
)
2
−
(
5
1
)
2
)
=
2
1
−
1
0
3
=
5
1
so
x
=
.
2
Consider the picture shown, the folded triangle has sides
2
1
and
1
and hypotenuse
2
5
, now from the small right triangle we have
cos
(
2
a
)
=
1
/
2
y
hence
x
=
2
1
−
y
=
2
1
−
2
1
cos
(
2
a
)
=
2
1
−
2
1
(
cos
2
a
−
sin
2
a
)
replacing we get
x
=
2
1
−
2
1
(
(
5
2
)
2
−
(
5
1
)
2
)
=
2
1
−
1
0
3
=
5
1
so
x
=
.
2
What is y?
Log in to reply
it's the length of the left side of the small right triangle marked in blue on the picture
Draw a line parallel to the lower side of the square through the red point. Because the right angle vertex is located at this point the two right triangles formed to the left and right of the point are similar with scale factor 1:2. Thus the proportion ((1/2) - d)/sqrt(1^ - (1 - d)^2) = 1/2 holds, which is equivalent to 5d^2 - 6d + 1 = (5d - 1)(d - 1) = 0. Since d < 1, it follows that d = 1/5.
The vector (-1,0) has been rotated by 53.4 degrees. multiply this by the rotation matrix that accounts for the rotation.
x = cos(53.4) * -1
y = sin(53.4) * -1
y is approximately -.8.
therefore the difference is approximately .2