Origami Paper Popping Time!

Classical Mechanics Level 2

Suppose you folded three rectangular papers of different sizes and same densities into origami paper poppers, as instructed above. Let A A be the smallest popper, B B the medium popper, and C C the largest popper. The goal is to have the inner flaps appear outside, as shown below:

If you are to apply the same force for each popper without tucking the inner flaps out, what can be said about their popping outcomes?

Details and Assumptions:

  • The creases of all three poppers are applied with the same amount of force.
  • The swings are executed in the same constant motion for all three poppers.
  • Your fingers still hold the tip of the popper after flicking it.
  • Neglect air resistance.
Image Credit: Wikimedia, Simply Bliss Life
A A has the highest chance of popping B B has the highest chance of popping C C has the highest chance of popping All poppers have the same chance of popping The outcomes depend on the poppers

View wiki
Michael Huang by Michael Huang , 29, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Michael Huang
Jan 20, 2017

The odds that the flaps pop vary for different sizes because of the amount of air trapped inside the pockets. For this solution, I would like to establish several relationships.

Consider the instructions to construct the paper popper.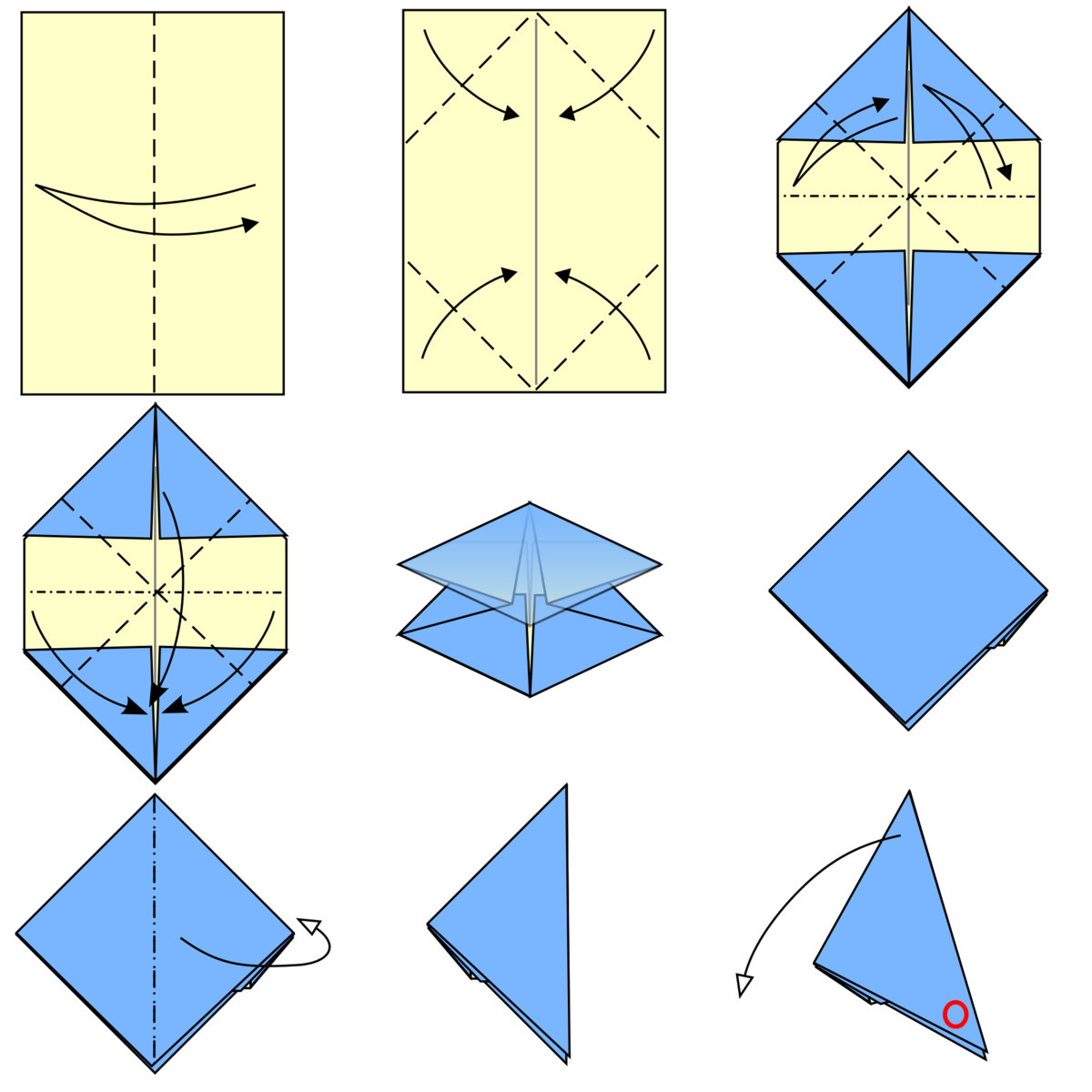

The relationship between the size of the popper and the size of the flaps is that:

  • The larger the popper size, the larger the flaps. Then, there is greater amount of flap space, therefore greater amount of air.
  • The smaller the popper size, the smaller the flaps. Then, there is less amount of flap space, therefore less amount of air.

Wherever your fingers hold on the indicated popper tip, this tightens the amount of opening space between the inner and outer flaps. Relative to the holding position,

  • For smaller poppers, there is greater amount of pressure inside the flaps, which requires very high velocity to produce the noise.
  • For larger poppers, there is less amount of pressure, which allows the air to fill the vacuum easily. In this case, it is easier to create the noise with largest poppers than smallest ones.

Related Examples: There are related real-life examples to come up with:

  • Imagine the balloons trapped with helium gas. The greater the volume, the greater the bursting chance. The smaller the volume, the lower the bursting chance. It is clear that if there is no air inside the balloon (which is of course very flimsy), the balloon is least likely to burst.
  • The interesting example that Mendrin mentioned. That is: consider three different sizes of the ships made out of the same materials and structures. Because the largest ship is more rigid than smallest ship, the largest one is most likely to break.
8 Helpful 0 Interesting 0 Brilliant 0 Confused
Michael Mendrin
Jan 19, 2017

Imagine we built 3 ocean ships of the same design but of different sizes, and yet using the same steel plate for the hull and structure. Which one is the most likely to break up in very rough waters? The largest one.

In a way, a ship's rigidity in face of forced flexure is similar to this question about paper poppers.

2 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...