Paper Problem

Geometry Level 2

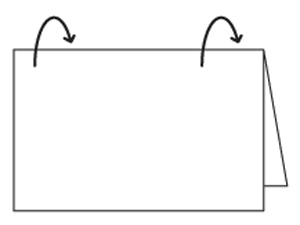
A sheet of regular A4 paper, folded in half, has the same ratio of side lengths than that of the original sheet (so it can be folded in half indefinitely and retain the same aspect ratio).

What is the ratio of the length of the paper to the width of the paper?

3-\sqrt{2}

\sqrt{2}

\phi

2

\sqrt{{e}}

3 solutions

Miksu Rankaviita
Jan 20, 2016

C'mon, everyone who have watched numberphile knows this

I had no idea there was an episode on this!

Fin Moorhouse - 5 years, 4 months ago

Well not an entire episode but they mentioned it in a video where they talked about $\sqrt{2}$

miksu rankaviita - 5 years, 4 months ago

Fin Moorhouse
Jan 20, 2016

Let the length of the longest side be $y$ , and the shortest be $x$ . The ratio of the two sides ( $\frac{y}{x}$ ) should be equal to the ratio of the sheet folded in half. The shortest side length of the folded sheet is $0.5y$ and the new longest side length is just $x$ . Therefore $\frac{y}{x}=\frac{x}{0.5y}$ . Multiply though by $0.5y$ : $\frac{0.5y^2}{x}=x$ , and then by $x$ : $0.5y^2=x^2$ which can be expressed as $y^2=2x^2$ . We can square root both sides: $y=\sqrt{2}x$ . Therefore $\frac{y}{x}=\sqrt{2}$ $\blacksquare$

It looks like you assumed that the length of half of the longest side is less than the length of the shortest side. I don't know the exact dimensions of an A4 paper, but I don't think that half of the longest side is necessarily shorter than the shortest side. I tried to find any hint in the question that might have prompted you to approach it as you just have done here, but I couldn't. In fact, I have difficulty of making out the meaning of the following expression:"...has the same ratio of lengths than the original one...( the same...than...)".

Solomon Hailu - 5 years, 4 months ago

It just ment that if you devide the longer side by the shorter side, you will get the same number as if you folded the A4 by half as shown in the picture and then devided the new longer side with the new shorter side

miksu rankaviita - 5 years, 4 months ago

I meant that the paper has the same ratio of side lengths when it is folded in half, which I reckon is fairly unambiguous.

Fin Moorhouse - 5 years, 4 months ago

Tom Whiteley
Nov 14, 2016

Yep Numberphile does a great explanation for why this is. If we label the long edge a, and short edge b, we want to find a constant ration between a and b if the paper folds in half, (so a becomes a/2). So, we assume that:

$\frac{a}{b}$ = $\frac{b}{(a/2)}$

This means that a $^2$ = 2b $^2$ from cross multiplication, then $\frac{a}{b}$ = $\sqrt{2}$

Paper Problem

3 solutions

0 pending reports