Para
The figure below shows a parallelogram with an area of 1. The green points are midpoints of two adjacent sides.
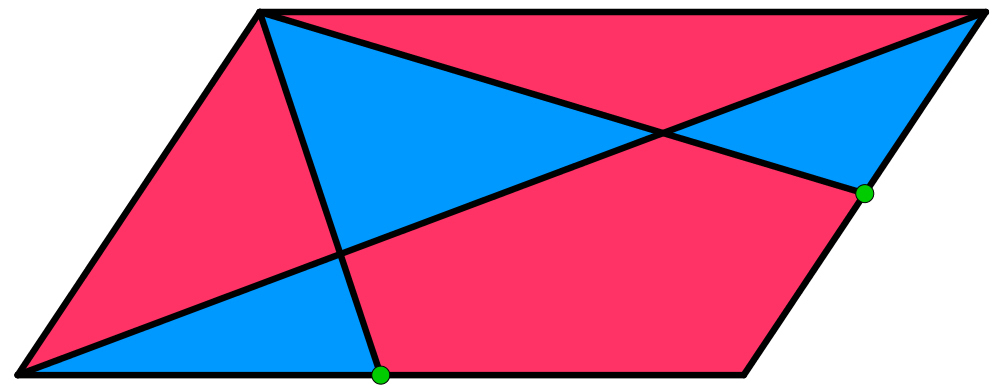
What is the sum of the blue areas?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
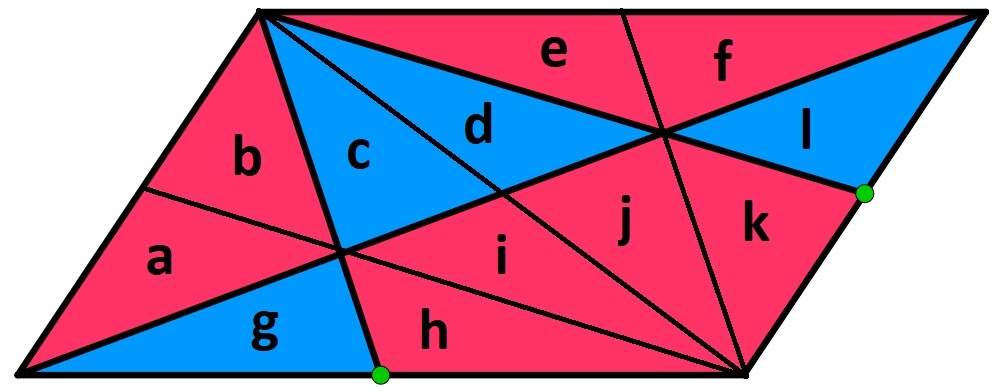 There are 12 equal triangles. Four of them make the blue area, which is 4/12, which is 1/3.
There are 12 equal triangles. Four of them make the blue area, which is 4/12, which is 1/3.
I see six pairs of same sized triangles. How do you get that they are all equal sized?
Let a , b , c , d , e , and f be the six areas, labeled below.
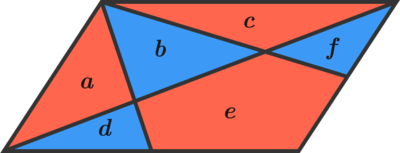
The diagonal splits the parallelogram into two halves, so
a + b + c d + e + f = 2 1 = 2 1
We also have the smaller triangles formed from areas at the left and on top,
a + d c + f = 4 1 = 4 1
Now consider that the triangle formed from area d and the triangle formed from areas b and c are similar. Likewise, the triangle formed from area f and the triangle formed from areas a and b are similar. This gives:
d f = 4 1 ( b + c ) = 4 1 ( a + b )
Now we have six distinct equations for the six unknowns. Solving the system gives
a b c d e f = 6 1 = 6 1 = 6 1 = 1 2 1 = 3 1 = 1 2 1
The total blue area is 6 1 + 1 2 1 + 1 2 1 = 3 1 .