Parabola
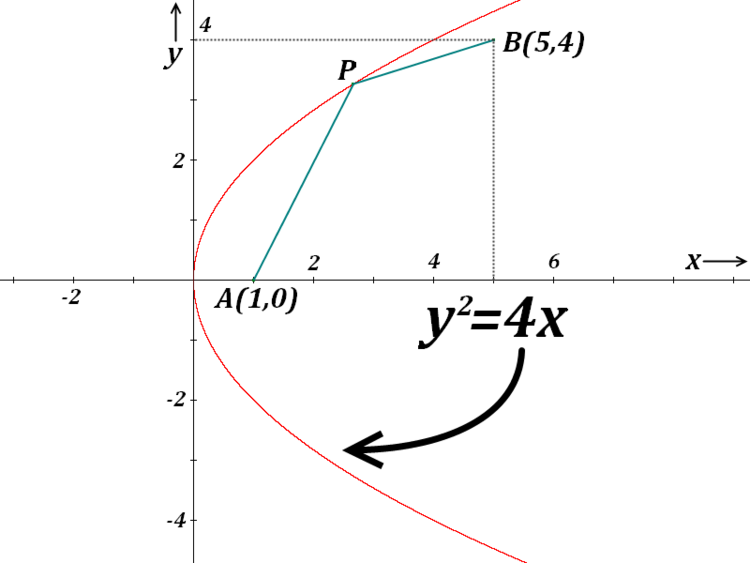 Consider two points
A (1,0)
, and
B (5,4)
. Point P (whose coordinate is unknown yet) lies somewhere on parabola
. As point P moves along the parabola, evaluate the
minimum possible value
of
.
Consider two points
A (1,0)
, and
B (5,4)
. Point P (whose coordinate is unknown yet) lies somewhere on parabola
. As point P moves along the parabola, evaluate the
minimum possible value
of
.
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The point A is the focus point of parabola y 2 = 4 x .
Therefore, the line P A is same as distance from point P to directrix of parabola y 2 = 4 x , which is x = − 1 .
Let the foot of perpendicular from point P to line x = − 1 be X. Therefore, the minimum possible distance of P A + P B is same as P X + P B .
Euclid postulate states that given any two point, the shortest distance between them is straight line. Therefore, minimum possible value of P X + P B would be the distance from foot of perpendicular from point B to line x = 1 to point B.
∴ min P A + P B = 5 + 1 = 6