Parabola and a Circle
A circle is tangent to the parabola y = x 2 , the x-axis y = 0 , and the line x = 6 7
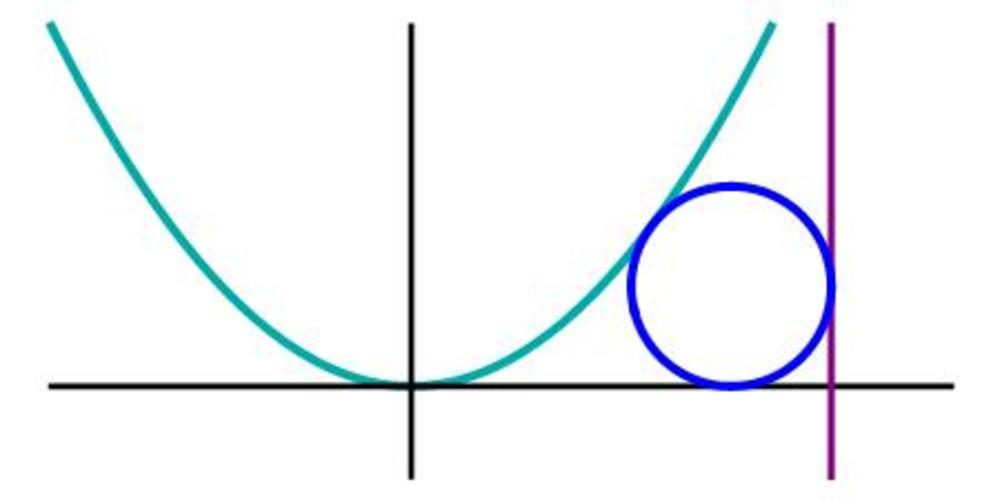
The radius of this circle can be expressed as b a where a , b are coprime integers.
Find sum a + b
The answer is 23.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
You have an interesting approach to these kinds of problems.
It actually ends up being relatively little work solving this way; the downside being that I have to guess the exact form from the numerical results (although I automate that process too).
Let r be the radius of the circle and let ( p , p 2 ) be the point of tangency between the parabola and the circle. Since the slope of any point on the parabola y = x 2 is y ′ = 2 x , the slope of the tangent line is 2 p , and since the hypotenuse of the given triangle is perpendicular to the tangent line, the sides of the triangle are t and 2 p t for some variable t .
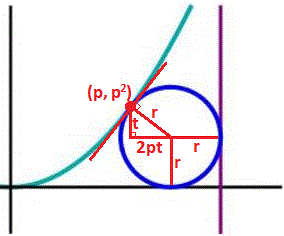
From the horizontal segments, p + 2 p t + r = 6 7 , and from the vertical segments, r + t = p 2 , and from Pythagorean's Theorem, t 2 + ( 2 p t ) 2 = r 2 .
These three equations solve to positive solutions of p = 3 2 , t = 6 1 , and r = 1 8 5 , so a = 5 , b = 1 8 , and a + b = 2 3 .
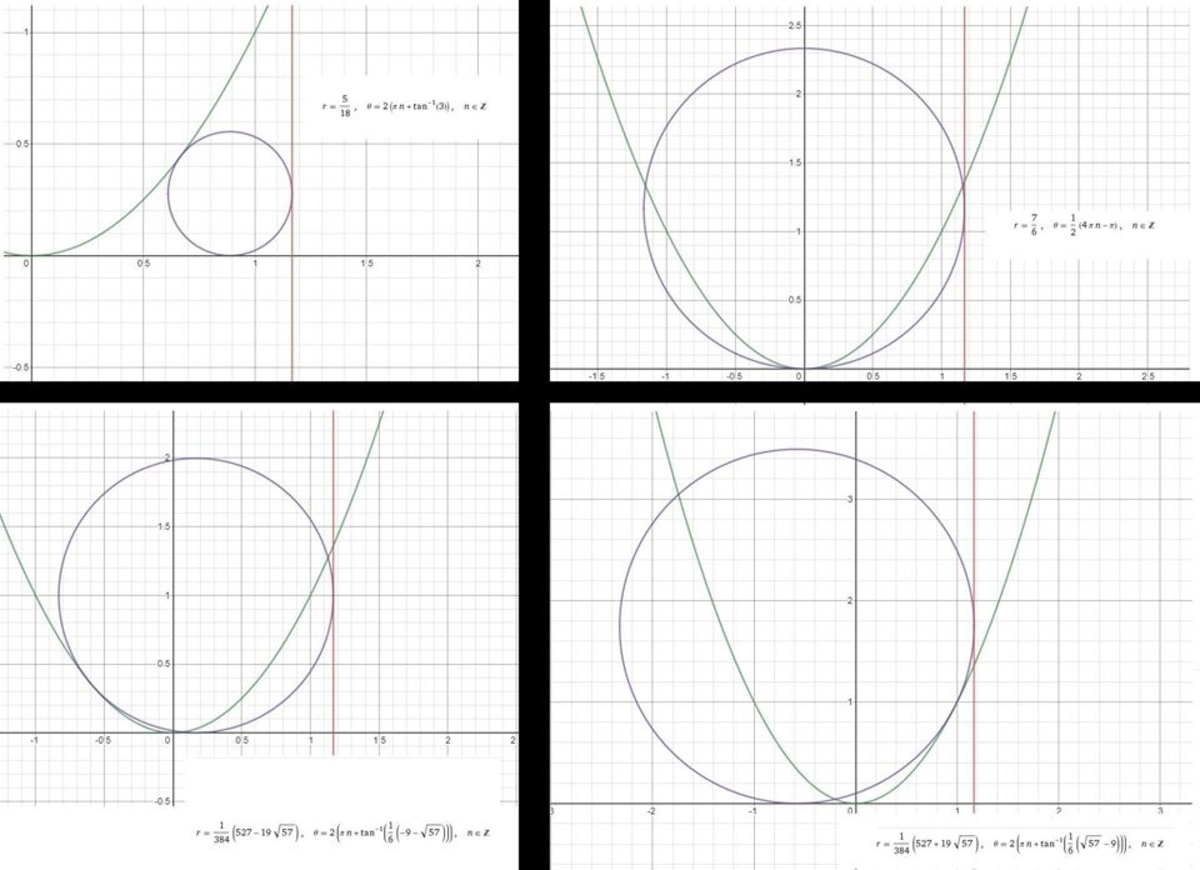
There are actually exist 4 solutions for this problem. Check the following graph !!
(by "Ragai Awad" one of my students)
The unknowns are the circle radius r and the and the x coordinate of the parabola tangent point. Define some tangential and normal unit vectors to the parabola at the tangent point:
T x = 1 + 4 x 2 1 T y = 1 + 4 x 2 2 x N x = T y N y = − T x
Then the equations to be satisfied are:
x + r N x + r = 6 7 x 2 + r N y − r = 0
Solving yields ( x , r ) = ( 3 2 , 1 8 5 )