Parabola and the minimum area

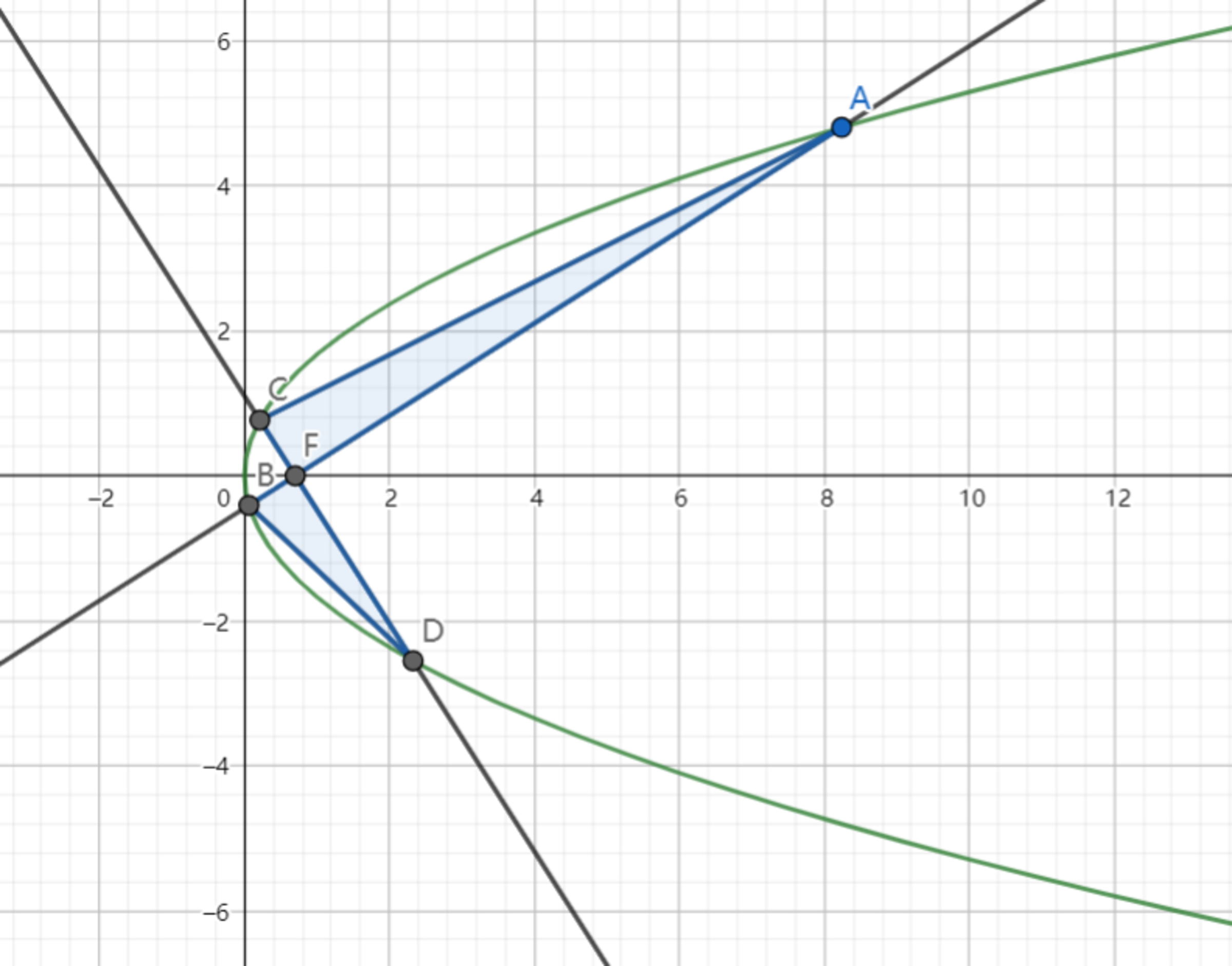
As shown above, on the coordinate plane, the parabola has equation: $y^2=2px (p>0)$ . Line $AB$ and $CD$ are perpendicular to each other and both pass through $F$ , the focus of the parabola.

If $S_{\triangle ACF}+S_{\triangle BDF}$ has the minimum value $8$ , then find the value of $p$ .

Note: $S_{\triangle ACF}, S_{\triangle BDF}$ denote the area of $\triangle ACF, \triangle BDF$ .