Parabola Halving a Triangle
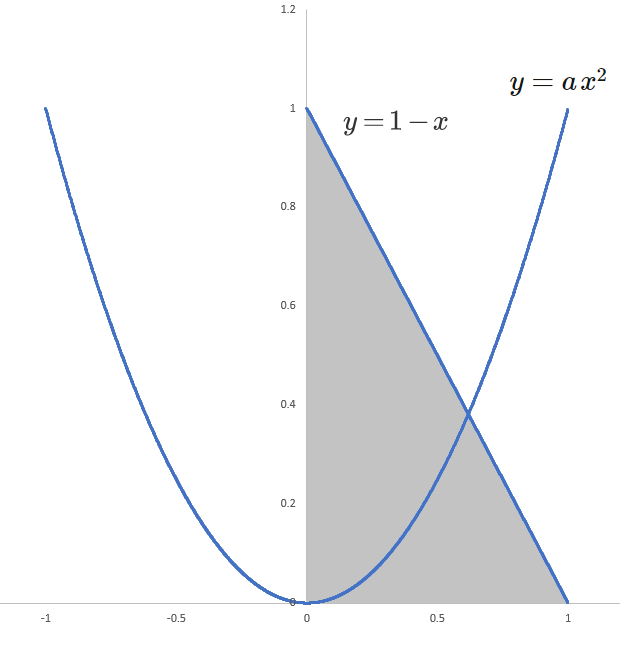
Consider a triangular region bounded by the x -axis, the y -axis, and the line y = 1 − x . The parabola y = a x 2 divides this region into two parts of equal area.
What is the value of a ?
The answer is 3.312.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Alternatively, you could solve for a in ∫ 0 ξ a x 2 d x + 2 1 ( 1 − ξ ) 2 = 4 1 .
Also, I think the 3 a in 1 2 a ( 4 a + 1 − 1 ) − 3 a ( 4 a + 1 − 1 ) 2 − ( 4 a + 1 − 1 ) 3 = 6 a 2 should just be a 3 .
Denote P ( β , a β 2 ) as the point where the line and the parabola meet, such that a β 2 = 1 − β
Clearly, the area of the triangle is 1 / 2 and the parabola divides the are into two regions each with area 1 / 4 .
∫ 0 β ( 1 − x − a x 2 ) d x β − 2 β 2 − 3 a β 3 β ( 1 2 − 6 β − 4 a β 2 ) β ( 1 2 − 6 β − 4 ( 1 − β ) ) 2 β 2 − 8 β + 3 β = 2 4 − 1 0 = 4 1 = 4 1 = 3 = 3 = 0
Note that β = 2 4 + 1 0 was not considered since we want 0 < = β < = 1 . Finally, a = β 2 1 − β = 9 1 4 + 5 1 0 ≈ 3 . 3 1 2 3 8
The key difference between this and Mark's solution is that I chose to solve for the root β first (in his case, ξ ) to reduce the algebraic expansions and manipulations involved.
The parabola and the line meet at the point with x -coordinate ξ , where 1 − ξ = a ξ 2 , and hence ξ = 2 a 4 a + 1 − 1 and we want ∫ 0 ξ ( 1 − x − a x 2 ) d x ξ − 2 1 ξ 2 − 3 1 a ξ 3 1 2 a ( 4 a + 1 − 1 ) − 3 ( 4 a + 1 − 1 ) 2 − ( 4 a + 1 − 1 ) 3 2 ( 4 a + 1 ) 4 a + 1 9 a 4 − 2 8 a 3 − 6 a 2 a 2 [ ( 9 a − 1 4 ) 2 − 2 5 0 ] = 4 1 = 4 1 = 6 a 2 = 6 a 2 + 1 2 a + 2 = 0 = 0 and hence, since a is positive, a = 9 1 4 + 5 1 0 = 3 . 3 1 2 3 8