Parabola Identification
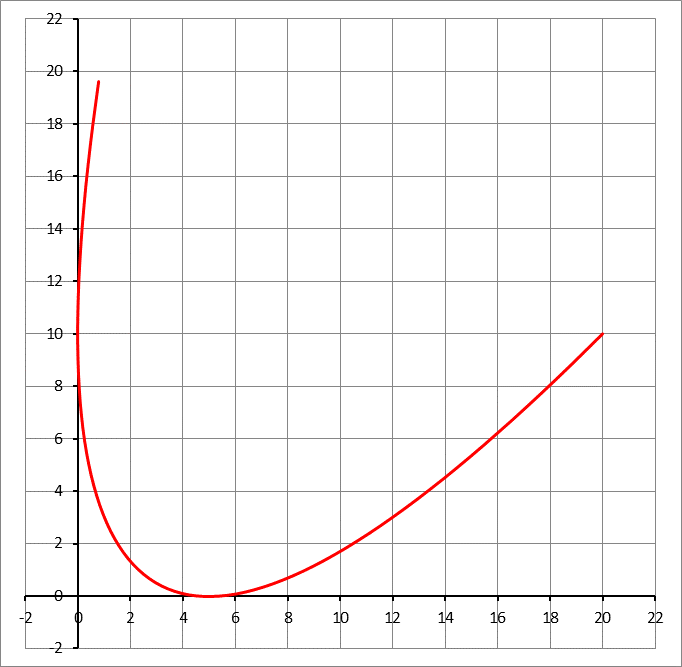
The parabola y = α x 2 is shifted to a new vertex ( x V , y V ) and rotated by an angle ψ ∘ clockwise about this new vertex, such that it is becomes tangent to the x -axis at ( 5 , 0 ) and to the y -axis at ( 0 , 1 0 ) . find the parameters of this parabola. Submit the value of 1 0 x V + 2 0 y V + 3 0 α + ψ . Note that ψ must be expressed in degrees.
One way to approach this problem is through Quadratic Bézier Curve
The answer is 70.75767863.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let the tangency points be ( a , 0 ) and ( 0 , b ) . Then a = 5 and b = 1 0 .
Using the Quadratic Bézier Curve method, the parametric equation of the parabola is
p ( t ) = P 0 ( 1 − t ) 2 + 2 t ( 1 − t ) P 1 + t 2 P 2
where P 0 , and P 2 are the endpoints , that is, P 0 = ( 0 , b ) , and P 2 = ( a , 0 ) and P 1 is the point where the tangents at these two points intersect, so P 1 = ( 0 , 0 ) . Substituting this, we have
p ( t ) = ( 0 , b ) ( 1 − t ) 2 + t 2 ( a , 0 ) = [ a t 2 , b ( 1 − t ) 2 ] = ( a , b ) t 2 + ( 0 , − 2 b ) t + ( 0 , b ) = v 2 t 2 + v 1 t + v 0
It is straight forward to find the vertex, if we use the property that at the vertex, p ˙ ( t ) ⋅ p ¨ ( t ) = 0 .
Differentiating once, p ˙ ( t ) = 2 ( − ( 0 , b ) ( 1 − t ) + t ( a , 0 ) ) = 2 ( a t , b ( t − 1 ) ) . Differentiating again, p ¨ ( t ) = 2 ( a , b ) . Hence, at the vertex, ( a , b ) ⋅ ( a t ∗ , b ( t ∗ − 1 ) ) = 0 . From this, t ∗ = a 2 + b 2 b 2 is the value of the parameter t at which the vertex occurs. Substituting in the values of a = 5 and b = 1 0 , yields t ∗ = 0 . 8 . Upon substituting this value in the parameteric curve, we get the coordinates of the vertex,
p V = ( 0 , 1 0 ) ( 0 . 2 ) 2 + ( 5 , 0 ) ( 0 . 8 ) 2 = ( 3 . 2 , 0 . 4 ) .
The next parameter we can obtain using t ∗ is the angle of rotation (clockwise) that the parabola was rotated through. That is because the axis of symmetry is orthogonal to the tangent at the vertex. The direction of the tangent at the vertex is given by:
p ˙ ( t ∗ ) = ( 5 ( 0 . 8 ) , 1 0 ( − 0 . 2 ) ) = ( 4 , − 2 )
Hence, the direction of the axis of symmetry of the parabola is along the perpendicular direction ( 1 , 2 ) . The angel of rotation ψ , is the angle that this last vector makes with the direction of the y - axis. This is given by
ψ = 9 0 ∘ − tan − 1 1 2 = 2 6 . 5 6 5 1 ∘
What is left is to find the coefficient α of the parabola. Starting with (see above),
p ( t ) = v 2 t 2 + v 1 t + v 0 , where v 2 = ( a , b ) , v 1 = ( 0 , − 2 b ) , and v 0 = ( 0 , b ) , we want to orthogonalize the vectors v 2 , v 1 , using Gram-Schmidt vector orthogonalization algorithm. We will take the first of the orthogonal set of unit vectors to be along v 2 . That is we set
u 1 = ∣ ∣ v 2 ∣ ∣ v 2
Next, we take the second vector along v 1 − ( v 1 ⋅ u 1 ) u 1 , and normalize it.
It can shown, after some simple manipulations, that the coefficient α is given by,
α = ∣ ∣ v 1 − ( v 1 ⋅ u 1 ) u 1 ∣ ∣ 2 ∣ ∣ v 2 ∣ ∣
This comes to,
α = 0 . 1 3 9 7 5 4 2 4 8 5 9 3 7 3 7
Adding up the given linear combination of the parameters gives the answer.
The formula for a conic is A x 2 + B x y + C y 2 + D x + E y + F = 0 . Since it passes through ( 5 , 0 ) , 2 5 A + 5 D + F = 0 , and since it passes through ( 0 , 1 0 ) , 1 0 0 C + 1 0 E + F = 0 . Using implicit differentiation on the conic equation gives 2 A x + B x d x d y + B y + 2 C y d x d y + D + E d x d y = 0 or d x d y = B x + 2 C y + E − 2 A x − B y − D . Since the parabola is tangent to the x -axis at ( 5 , 0 ) , d x d y = 0 at ( 5 , 0 ) , and so 1 0 A + D = 0 , and since the parabola is tangent to y -axis at ( 0 , 1 0 ) , d x d y is undefined at ( 0 , 1 0 ) , and so 2 0 C + E = 0 . Finally, as a parabola, B 2 − 4 A C = 0 .
Solving this system of equations gives B = ± A , C = 4 1 A , D = − 1 0 A , E = − 5 A , and F = 2 5 A and so the conic equation becomes A x 2 ± A x y + 4 1 A y 2 − 1 0 A x − 5 A y + 2 5 A = 0 , or x 2 ± x y + 4 1 y 2 − 1 0 x − 5 y + 2 5 = 0 for A = 0 . When B = + A the conic equation degenerates to a line, and so B = − A , and so the conic equation is x 2 − x y + 4 1 y 2 − 1 0 x − 5 y + 2 5 = 0 .
This makes the clockwise angle of rotation ψ = 2 1 tan − 1 1 − 4 1 1 = 2 1 tan − 1 3 4 . Using the tangent half-angle equation, ψ = tan − 1 1 + 3 2 + ( − 4 ) 2 3 3 2 + ( − 4 ) 2 − 4 = tan − 1 2 1 .
Since tan ψ = 2 1 , d x d y = − 2 1 at the parabola's vertex. With this slope, our previous equation 2 A x + B x d x d y + B y + 2 C y d x d y + D + E d x d y = 0 now simplifies to y = 2 x − 6 , and this and the conic equation x 2 − x y + 4 1 y 2 − 1 0 x − 5 y + 2 5 = 0 intersect at the vertex ( 5 1 6 , 5 2 ) , which makes V x = 5 1 6 and V y = 5 2 .
Finally, a rotation of ψ = tan − 1 2 1 gives a new rotated parabola of 4 5 x 2 − 3 5 x − 4 5 y + 2 5 = 0 , which rearranges to y = 1 6 5 ( x − 5 6 5 ) 2 + 5 4 5 , and so α = 1 6 5 .
Therefore, 1 0 V x + 2 0 V y + 3 0 α + ψ = 1 0 ( 5 1 6 ) + 2 0 ( 5 2 ) + 3 0 ( 1 6 5 ) + tan − 1 2 1 ≈ 7 0 . 7 5 7 6 7 8 6 3 .