Parabola to Circle
Consider all parabolas of the form y = x 2 + 2 p x + q for p , q ∈ R which intersect the coordinate axes in three distinct points. For such p , q , denote by C p , q the circle through these three intersection points. All these circles C p , q have a point ( a , b ) in common. Find the value of a + b .
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
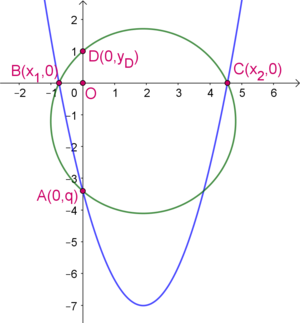 Since the coefficient of
x
2
in the quadratic is positive, the parabola intersects the y-axis at a point of negative ordinate. Moreover, the two distinct points of intersection of the parabola with the x-axis have opposite signs. Thus, every circle
C
p
,
q
has a second common point with the y-axis, which belongs to the positive half-axis
O
y
. Label the four points where an arbitrary circle
C
p
,
q
cuts the axes as shown in the figure.
If
x
1
,
x
2
are the roots of the quadratic equation
x
2
+
2
p
x
+
q
=
0
, with
x
1
<
x
2
, then the points are
A
(
0
,
q
)
,
B
(
x
1
,
0
)
,
C
(
x
2
,
0
)
a
n
d
D
(
0
,
y
D
)
Using the
power of a point theorem
(also called
Intersecting Chords Theorem
) we have
O
B
⋅
O
C
=
O
A
⋅
O
D
⇒
(
−
x
1
)
⋅
x
2
=
−
q
⋅
y
D
⇒
y
D
=
x
1
x
2
q
⇒
y
D
=
1
by Vieta’s Formula for Quadratics
This means that the fixed point
D
(
0
,
1
)
belongs to any circle
C
p
,
q
.
For the answer,
a
+
b
=
0
+
1
=
1
.
Since the coefficient of
x
2
in the quadratic is positive, the parabola intersects the y-axis at a point of negative ordinate. Moreover, the two distinct points of intersection of the parabola with the x-axis have opposite signs. Thus, every circle
C
p
,
q
has a second common point with the y-axis, which belongs to the positive half-axis
O
y
. Label the four points where an arbitrary circle
C
p
,
q
cuts the axes as shown in the figure.
If
x
1
,
x
2
are the roots of the quadratic equation
x
2
+
2
p
x
+
q
=
0
, with
x
1
<
x
2
, then the points are
A
(
0
,
q
)
,
B
(
x
1
,
0
)
,
C
(
x
2
,
0
)
a
n
d
D
(
0
,
y
D
)
Using the
power of a point theorem
(also called
Intersecting Chords Theorem
) we have
O
B
⋅
O
C
=
O
A
⋅
O
D
⇒
(
−
x
1
)
⋅
x
2
=
−
q
⋅
y
D
⇒
y
D
=
x
1
x
2
q
⇒
y
D
=
1
by Vieta’s Formula for Quadratics
This means that the fixed point
D
(
0
,
1
)
belongs to any circle
C
p
,
q
.
For the answer,
a
+
b
=
0
+
1
=
1
.
@Thanos Petropoulos , we really liked your comment, and have converted it into a solution.
Log in to reply
Thank @Brilliant Mathematics ! I was about to ask for some help, but you are faster than your shadow :)
Starting with,
y = x 2 + 2 p x + q = ( x + p ) 2 + q − p 2
The x-intercepts are,
P 1 = ( − p − p 2 − q , 0 )
P 2 = ( − p + p 2 − q , 0 )
and the y-intercept is P 3 = ( 0 , q )
The center of circle passing through P 1 , P 2 and P 3 is C = ( − p , h ) , where h is found by setting,
∣ C P 1 ∣ 2 = ∣ C P 3 ∣ 2
that is,
p 2 − q + h 2 = p 2 + h 2 − 2 h q + q 2
Simplifying
h = 2 1 ( q + 1 )
So, now we have the center coordinates,
C = ( − p , 2 1 ( q + 1 ) )
Equation of the circle, is given by,
( x + p ) 2 + ( y − 2 1 ( q + 1 ) ) 2 = r 2
Plugging in P 3 = ( 0 , q ) , we get
p 2 + ( 2 1 ( q − 1 ) ) 2 = r 2
and hence, the equation of the circle for any p, and q is
( x + p ) 2 + ( y − 2 1 ( q + 1 ) ) 2 = p 2 + ( 2 1 ( q − 1 ) ) 2
The invariant point ( a , b ) can be found by differentiating the circle equation with respect to p and q and setting the derivatives to zero.
Differentiating with respect to p
2 ( a + p ) ( ∂ p ∂ a + 1 ) + 2 ( b − 2 1 ( q + 1 ) ) ( ∂ p ∂ b ) = 2 p
Plugging in ∂ p ∂ a = ∂ p ∂ b = 0 , the above equation becomes,
2 ( a + p ) = 2 p
from which it follows that a = 0
Secondly, differentiating the circle equation with respect to q ,
2 ( a + p ) ( ∂ q ∂ a ) + 2 ( b − 2 1 ( q + 1 ) ) ( ∂ q ∂ b − 2 1 ) = 2 1 ( q − 1 )
Plugging in ∂ q ∂ a = ∂ q ∂ b = 0 , results in,
− ( b − 2 1 ( q + 1 ) ) = 2 1 ( q − 1 )
from which, b = 1
Therefore, the common point is ( a , b ) = ( 0 , 1 ) , and the answer is 0 + 1 = 1 .
From y = x 2 + 2 p x + q , the y -intercept is when x = 0 or y 0 = q . And the x -intercepts are given by x 2 + 2 p x + q = 0 or x 0 = − p ± p 2 − q . Let the center of circle C p q be C ( u , v ) and its radius be r . Then we have:
⎩ ⎨ ⎧ ( u − 0 ) 2 + ( v − y 0 ) 2 = u 2 + ( v − q ) 2 = r 2 ( u − x 0 ) 2 + ( v − 0 ) 2 = ( u + p ± p 2 − q ) 2 + v 2 = r 2 . . . ( 1 ) . . . ( 2 )
It is obvious that u = 2 x 0 + x 1 = − p . And
{ ( 1 ) : ( 2 ) : p 2 + v 2 − 2 q v + q 2 = r 2 p 2 − q + v 2 = r 2 . . . ( 3 ) . . . ( 4 )
From ( 3 ) − ( 4 ) : q − 2 q v + q 2 = 0 ⟹ v = 2 1 + q ; from ( 1 ) : r 2 = p 2 + ( 2 1 − q ) 2 ; and the equation of C p q is:
( x + p ) 2 + ( y − 2 1 + q ) 2 p 2 + ( y − 2 1 + q ) 2 ( y − 2 1 + q ) 2 y 2 − ( 1 + q ) y + 4 1 + 2 q + q 2 y 2 − ( 1 + q ) y + q ( y − 1 ) ( y − q ) = p 2 + ( 2 1 − q ) 2 = p 2 + ( 2 1 − q ) 2 = ( 2 1 − q ) 2 = 4 1 − 2 q + q 2 = 0 = 0 when x = 0
So we note that the point ( 0 , 1 ) is in every C p q . Therefore a + b = 0 + 1 = 1 .
[ This comment has been converted into a solution ]
@Thanos Petropoulos , too bad. It has happened to me too. As only a moderator, I cannot help but a Brilliant staff can.
Log in to reply
Thank you Chew-Seong! I'll try to get some help from Brilliant staff.
Log in to reply
Hi Thanos, feel free to tag me to get my attention. :)
Excellent solution by @Thanos Petropoulos , thanks for sharing it.
Log in to reply
@Hosam Hajjir - Thank you Hosam! One could suspect that the common point would be on the y-axis (due to symmetry of the various positions the parabola takes). The rest comes easily. I'm glad you like the solution.