Parabola's Golden Bridge
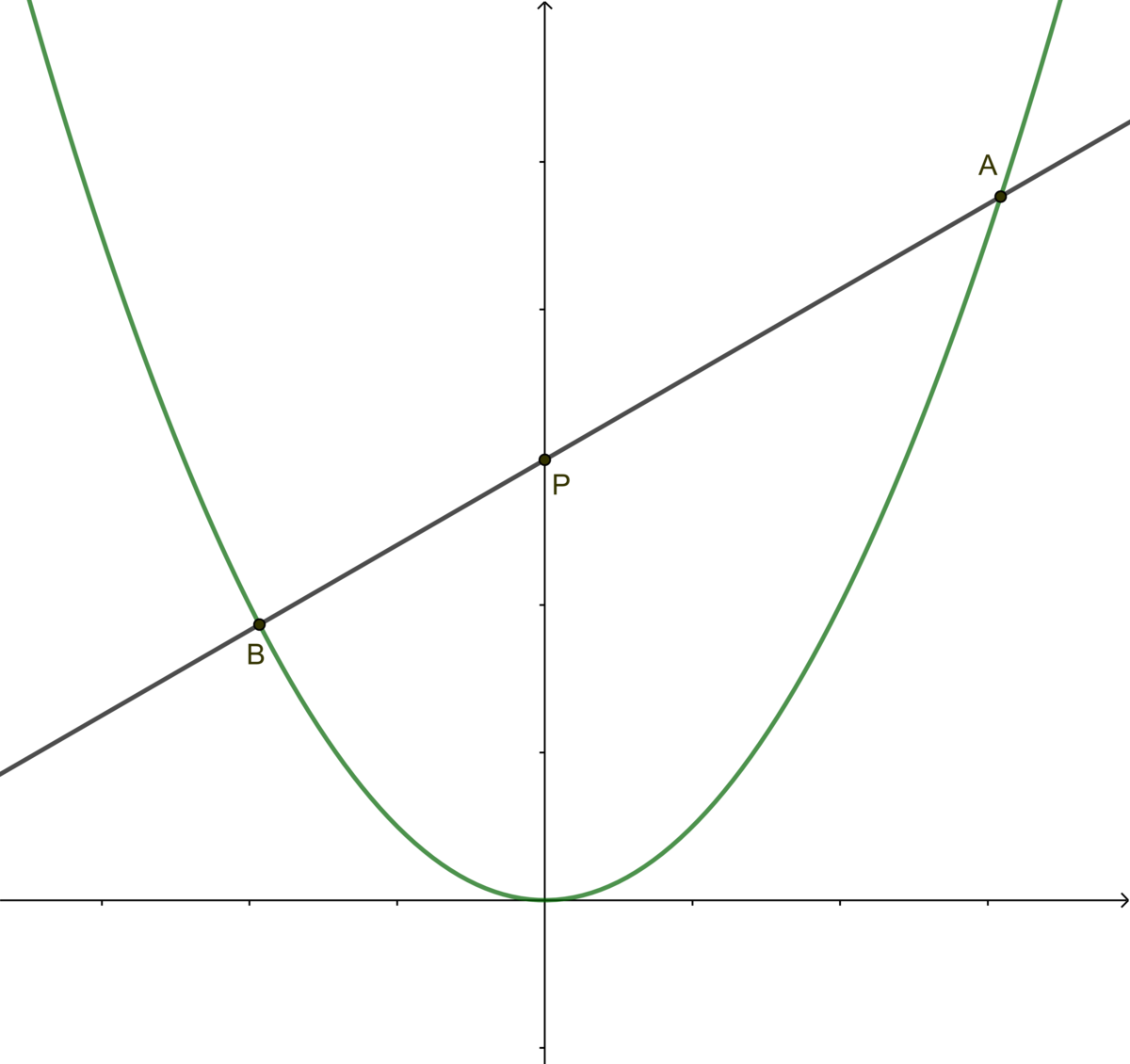
A line y = m x + c intersects parabola y = x 2 in points A and B . Line A B intersects y -axis at point P . ∣ A P − B P ∣ = 1 .
If m 2 can be expressed as r p + q , where p , q , r are integers with p square-free, enter the answer as p + q + r .
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Since the solution apparently must be independent of c , we'll just look for that point on the parabola x 2 that is at a distance of 1 from the origin. We then have the following to solve:
x 2 + x 4 = 1
which has as a solution
x = 2 5 − 1
leading us to the slope of the line from the origin to that point, which is the same as x 2 / x = x
If we do an affine transform of this parabola, plotting the following equation, we'll end up with the plot below, where the independence of c becomes obvious.
y = ( k x ) 2 − k x 2 1 ( 5 − 1 )
where
k = 2 1 ( 5 − 1 )
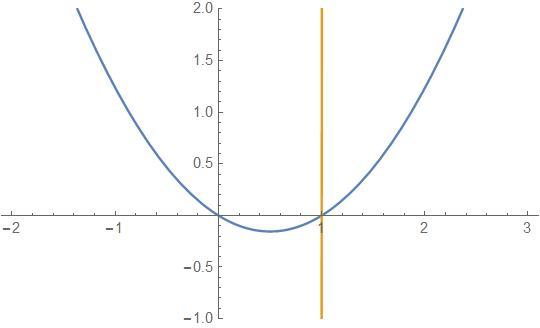
It certainly gets the value. It also means that unit circle will intersect parabola at the height of ϕ − 1 . Is it not all amazing?
Log in to reply
I seem to recall somewhere about an affine transform of the parabola that neatly explains the independence from c. Let me think about that one.
Okay, I've added comments about that to my solution. Check it out.
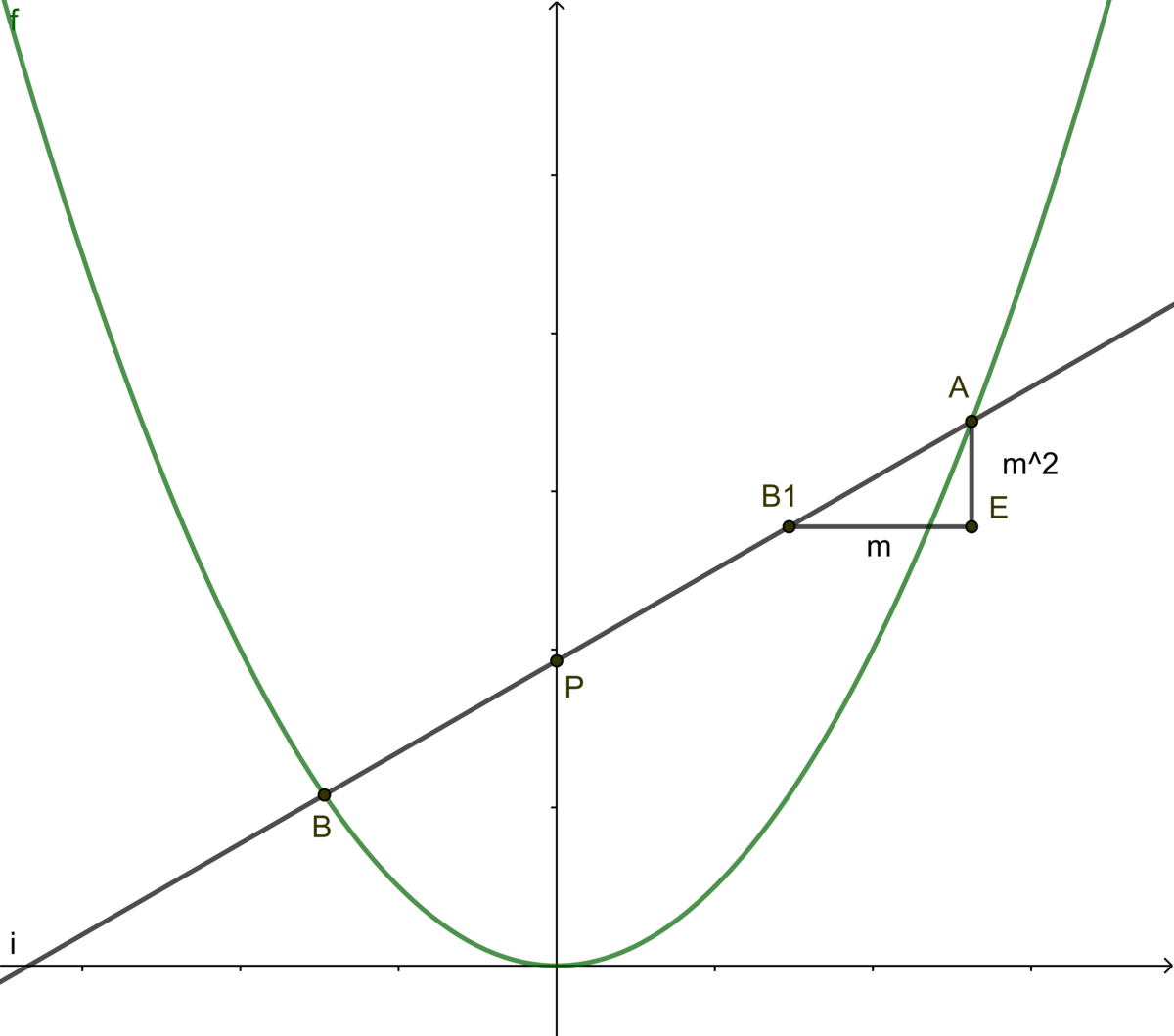
Let A ( a , a 2 ) and B ( b , b 2 ) .
Point B is reflected about point P giving point B 1 .
m = a − b a 2 − b 2 = a + b = B 1 E
m = B 1 E A E ⇒ A E = m 2 ⇒ A B 1 = A P − B P = ∣ m ∣ m 2 + 1
This means that this difference in lengths is constant for a given slope, regardless of the value of c .
∣ m ∣ m 2 + 1 = 1 ⇒ m 2 = 2 5 − 1 ⇒ p + q + r = 5 − 1 + 2 = 6
Note: Inspired by Is there an elegant method?
We have,
y = m x + c = x 2
which has two solutions x 1 , x 2 with x 1 > 0 and x 2 < 0 , the corresponding y-coordinates are,
y 1 = m x 1 + c
y 2 = m x 2 + c
Hence, we have,
A P = x 1 2 + ( y 1 − c ) 2 = x 1 1 + m 2
B P = x 2 2 + ( y 2 − c ) 2 = − x 2 1 + m 2
from which,
∣ A P − B P ∣ = ( x 1 + x 2 ) 1 + m 2
but from Vieta's formula applied to x 2 − m x − c = 0 , we know that x 1 + x 2 = m
Hence, m 1 + m 2 = 1
Squaring, m 2 ( 1 + m 2 ) = 1
Solving for m 2 using the Quadratic formula, we obtain
m 2 = 2 − 1 + 5
Hence, p = 5 , q = − 1 , r = 2 , making the answer 5 − 1 + 2 = 6 .