Extremum Accelerometer
A smooth wire is bent into the shape of a parabola. If the origin is taken to be the lowest point on the wire, x and y are related by y = x 2 . The wire starts accelerating to the right with acceleration a . Suppose the value of x ss , the steady state location of the bead in the coordinates of the wire, is − 3 0 c m .
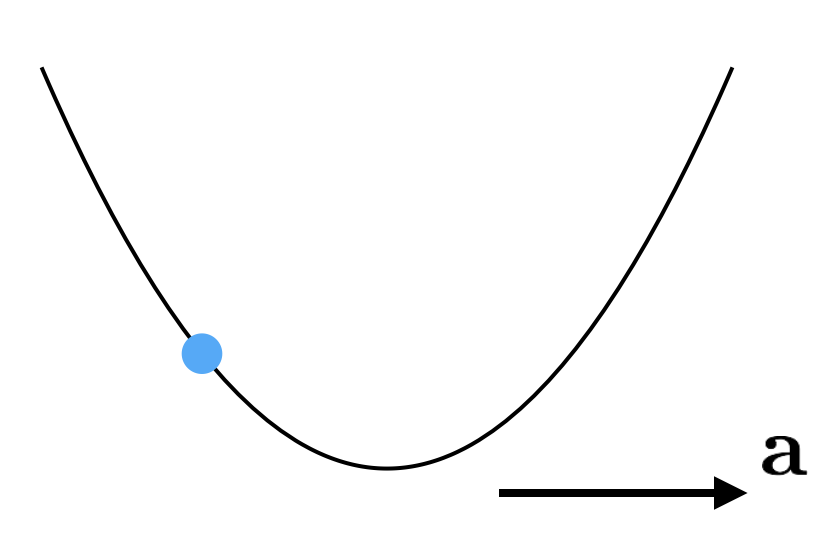
Find the acceleration a (in m / s 2 ) of the wire toward the right.
Details and Assumptions:
- g = 1 0 m / s 2 .
The answer is 6.0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
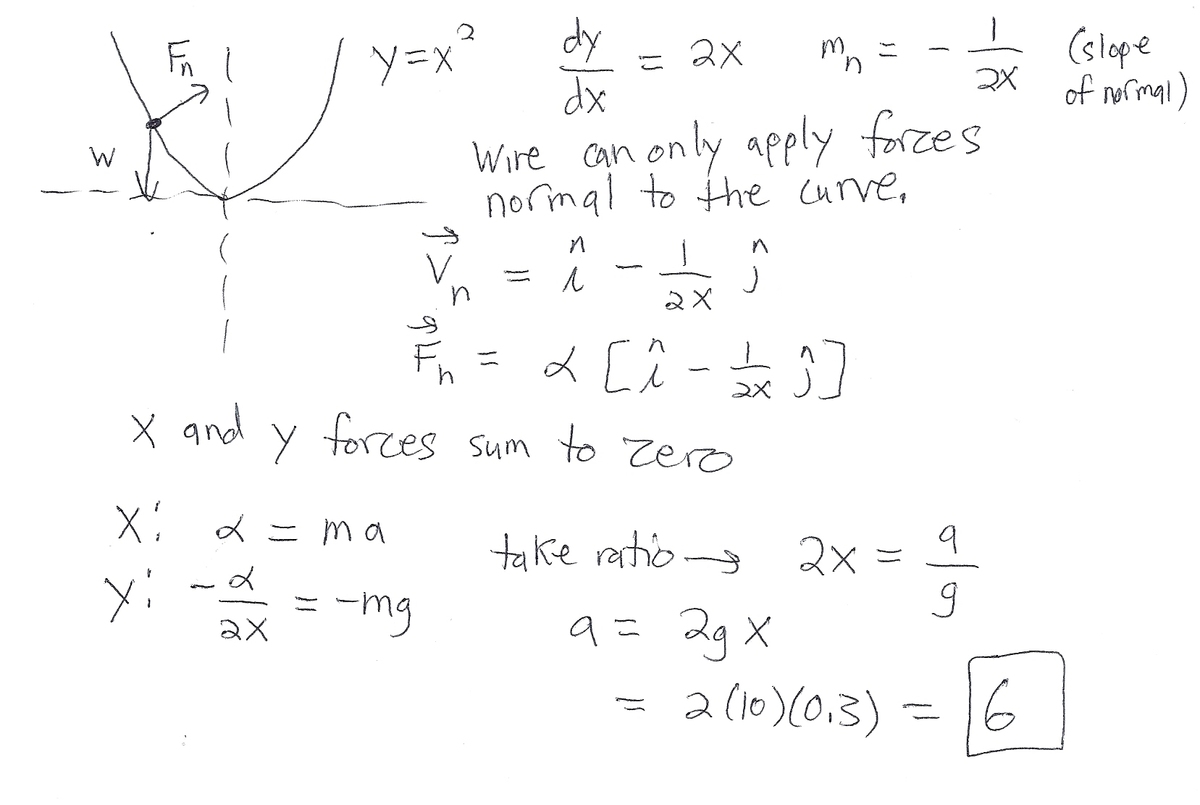
Could you please tell what is v<n>?
I really like this question! We basically just have to setup the equilibrium conditions for the forces acting on the bead. For simplicity, let's resolve the forces so that they are either tangent or normal to the parabola. Naturally, the perpendicular forces will automatically balance, as the normal force will supply the necessary force to counteract the perpendicular components of gravity and the rightward acceleration. Now, let's look at the forces tangent to the parabola. We know the bead is in equilibrium, so the tangent force supplied by gravity and the tangent force supplied by acceleration must be equal. Thus we have:
F a ( tangent ) = F g ( tangent )
Now, the slope of the line tangent to our equilibrium point, x s s , will be the derivative of the parabola at that point, thus:
dx d x 2 = 2 x ⇒ 2 x s s
And the right triangle formed by the tangent and the x-axis has an angle (between these two lines) of:
θ = tan − 1 2 x s s
As tan = a o = Δ x Δ y . By inspecting the angles (and doing some simple angle geometry), we find that in order to get the parallel components of the two forces, we multiply F g by sin θ and F a by cos θ . This means that we have:
m
a
cos
θ
=
m
g
sin
θ
⇒
m
a
cos
(
tan
−
1
2
x
s
s
)
=
m
g
sin
(
tan
−
1
2
x
s
s
)
⇒
a
=
g
tan
(
tan
−
1
2
x
s
s
)
=
2
g
x
s
s
=
(
2
)
(
1
0
)
(
0
.
3
)
=
6
m/s
2
