Parabolic Billiard

Geometry Level 4

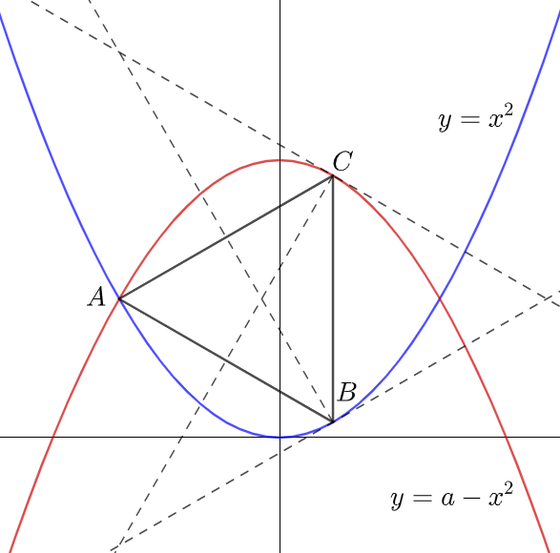
In the rectangular plane, the particle deflects two parabolas - the blue curve represented by $y = x^2$ and the red curve represented by $y = a - x^2$ for some real constant $a$ . It starts at the intersection point $A$ , passes through two symmetric reflection points $B$ and $C$ (about the horizontal) and travels back at $A$ , which forms an equilateral triangle. As shown, those dashed lines as angle bisectors indicate the particle reflects at the same angle to the normal. It can be shown that the side length of the triangle is $\dfrac{b}{c}$ , where $b$ and $c$ are both coprime positive integers. Find the value of $b + c$ .

Assumption: Treat the particle as a point.

The answer is 7.

2 solutions

David Vreken
Jun 7, 2021

Let the coordinates of $A$ be $(a, a^2)$ and $B$ be $(b, b^2)$ , and let $s = AB = BC = AC$ .

By symmetry, the tangent line at $B$ must have a slope of $m = \tan^{-1} 30° = \frac{\sqrt{3}}{3}$ , and by its derivative, $m = \frac{dy}{dx} = 2x = 2b$ at $B$ , so $m = \frac{\sqrt{3}}{3} = 2b$ , or $b = \frac{\sqrt{3}}{6}$ .

From the equilateral triangle, $A_x = a = b - \frac{\sqrt{3}}{2}s = \frac{\sqrt{3}}{6} - \frac{\sqrt{3}}{2}s = \frac{\sqrt{3}}{6}(1 - 3s)$ and $A_y = a^2 = b^2 + \frac{1}{2}s = \frac{1}{12} + \frac{1}{2}s = \frac{1}{12}(1 + 6s)$ .

That means $a^2 = (\frac{\sqrt{3}}{6}(1 - 3s))^2 = \frac{1}{12}(1 + 6s)$ , which solves to $s = \frac{4}{3}$ . Therefore, $b = 4$ , $c = 3$ , and $b + c = \boxed{7}$ .

Saya Suka
Jun 12, 2021

This is solvable just using the answer input space (unfortunately, not a last page margin as Fermat did once) only because it has an equilateral triangle in it. I'd surrender against a pentagonal one but a square might be easier, perhaps?

Parabolic Billiard

The answer is 7.

2 solutions

0 pending reports