Parabolic Conic Section
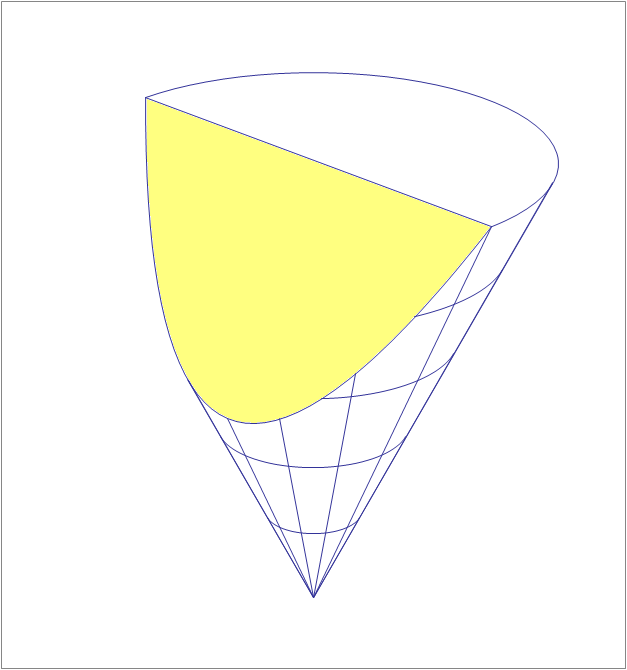
A cone of altitude 20 and an apex angle of (This is the angle between the axis of the cone and its lateral surface), is cut by a plane oriented in such a way to produce a parabolic section. If the lower point of the cut is half the slant height away from the apex, then find the area of the parabolic section (shaded yellow) to 2 decimal places.
The answer is 149.07.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let us call the the z -axis the axis of the cone altitude, x -axis the axis of the beginning of the cut and as y -axis the axis perpendicular to the x -axis.
Also, let us define three points: A and B the two extreme upper points of the parabola (the two ends of the cut) and C its lower point.
The distance d from any point on the circumference of the base to its center is:
2 0 d = t a n ( θ 0 ) = 2 1
d = 1 0
Since the lower point of the cut is halfway from the height, the distance between the cone center axis and point C will also be halfway between the cone center axis and its most external points, along the circumference of the base.
So, in this coordinate system, we have the following coordinates for these points:
( A ) : ( 1 0 , 0 , 2 0 )
( B ) : ( − 1 0 , 0 , 2 0 )
( C ) : ( 0 , − 5 , 1 0 )
If we look at these three points belonging to a new x y plane, considering C as the origin, we will have that x coordinate of A will be 1 0 , x coordinate of B will be − 1 0 , and the distance A B will be equal to A C , equal to:
A B = A C = ( 1 0 − 0 ) 2 + ( − 1 0 − 0 ) 2 + ( 2 0 − 1 0 ) 2
A B = A C = 1 5
So, the y coordinate of A and B will be:
y A = y B = 1 5 2 − 1 0 2
y A = y B = 5 5 .
The parabola has its minimum at the origin. Hence, its equation is like y = a x 2 . Since it passes through A and B :
5 5 = a ⋅ ( ± 1 0 ) 2
a = 2 0 5
Finally, the area S we're looking for is the area inside of the parabola:
S = ∫ − 1 0 1 0 ( 5 5 − 2 0 5 x 2 ) d x
S = 5 5 x ∣ ∣ ∣ − 1 0 1 0 − 6 0 5 x 3 ∣ ∣ ∣ − 1 0 1 0
S = 1 0 0 5 − 3 1 0 0 5
S = 3 2 0 0 5 ≈ 1 4 9 . 0 7 . . .