Parabolic Eye
A parabola y = x 2 is capped by another parabola of the form y = a − b x 2 that is orthogonal to the first, i.e., they intersect at right angles , A circle is inscribed tangent to both in three places.
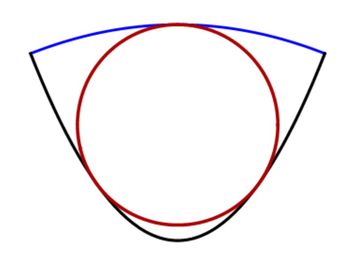
The diameter of that inscribed circle is such that it covers the maximum fraction of the area between the two parabolas.
This diameter can be expressed as p . Find p .
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The most surprising thing about this problem is that the optimum is not the trivial case of two equal parabolas.
Log in to reply
Astounding
I guess the asymmetry of the solution comes from the asymmetry of the tangency conditions - but it is surprising that the optimum isn't achieved in the limiting case when the two tangency points on P 1 coincide.
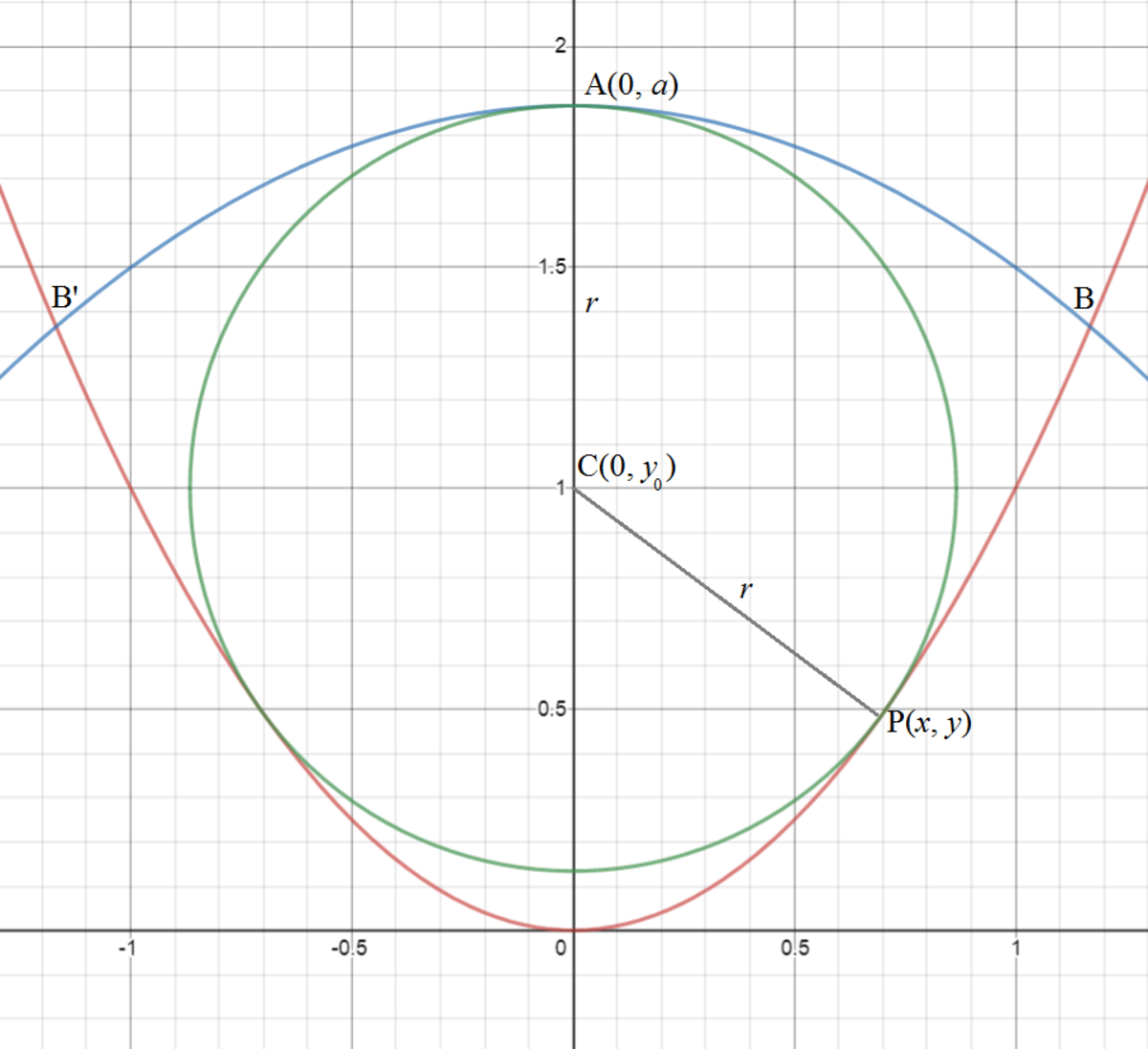
Let A ( 0 , a ) be the vertex of y = a − b x 2 , B and B ′ be the points the two parabolas intersect, C ( 0 , y 0 ) the center of the circle and r its radiux, and P ( x , y ) the point in the positive quadrant where the circle touches y = x 2 .
The point P ( x , y ) satisfies both { x 2 + ( y − y 0 ) 2 = r 2 y = x 2 ⟹ y + ( y − y 0 ) 2 = r 2 . The gradients of the circle and parabola at P are the same. For the circle d x d y + 2 ( y − y 0 ) d x d y = 0 . Since d x d y = 2 x = 0 , ⟹ y − y 0 = − 2 1 and y = y 0 − 2 1 = a − r − 2 1 , as y 0 = a − r . Then we have:
y + ( y − y 0 ) 2 a − r − 2 1 + 4 1 ⟹ a = r 2 = r 2 = r 2 + r + 4 1 = ( r + 2 1 ) 2
When the two parabolas intersect, we have a − b x 2 = x 2 ⟹ x B = ± b + 1 a . Since the parabolas intersect orthogonally, the product of their gradients is − 1 . That is ( − 2 b x B ) ( 2 x B ) = − 1 or:
( − 2 b b + 1 a ) ( 2 b + 1 a ) 4 a b ⟹ b = − 1 = b + 1 = 4 a − 1 1
Note that the area enclosed by a parabola is (\frac 23) the area of rectangle inscribing it. Therefore the area of the area enclosed by the two parabolas is directly proportional to a b + 1 a = a 4 a b a = a a − 4 1 . Since the area of the circle is directly proportional to r 2 , we need to find r when a a − 4 1 r 2 is maximum or r 2 a a − 4 1 is minimum.
f ( r ) d r d f ( r ) = r 2 a a − 4 1 = r 2 ( r + 2 1 ) 2 r ( r + 1 = ( r + 1 + 4 r 1 ) 1 + r 1 = ( 1 − 4 r 2 1 ) 1 + r 1 − 2 r 2 1 + r 1 r + 1 + 4 r 1
Equating d r d f ( r ) to zero.
2 r 2 ( 1 − 4 r 2 1 ) ( 1 + r 1 ) 8 r 3 + 4 r 2 − 6 r − 3 ( 2 r − 3 ) ( 2 r + 3 ) ( 2 r + 1 ) ⟹ r 2 r = r + 1 + 4 r 1 = 0 = 0 = 2 3 = 3 Since r > 0
Therefore, p = 3 .
Call the black parabola P 1 , the blue parabola P 2 , and the circle C .
These curves have the following equations:
P 1 P 2 C : y = x 2 : y = a − b x 2 : x 2 + ( y − c ) 2 = r 2
where r is the radius of C and its centre (which, by symmetry, is on the y -axis) is ( 0 , c ) .
P 1 and P 2 intersect when x 2 = a − b x 2 , that is when x = ± b + 1 a
The gradient of P 1 is 2 x ; the gradient of P 2 is − 2 b x . Since they are orthogonal, the product of their gradients at their intersections is − 1 ; by symmetry we can just look at the positive intersection to get
( 2 b + 1 a ) ⋅ ( − 2 b b + 1 a ) = − 1
which after tidying up becomes
b = 4 a − 1 1
which means the positive intersection point is at x = 2 1 4 a − 1 .
Now let's look at C . It touches P 2 at the point ( 0 , a ) ; so we have
c = a − r
(where we've used the geometry to discard the case c = a + r .)
It is also tangent to P 1 . The intersections of C and P 1 are found by plugging y = x 2 into the equation for C ; that is at the intersection points
y + ( y − c ) 2 = r 2
Expanding, this is
y 2 + ( 1 − 2 c ) y + c 2 − r 2 = 0
Since C is tangent to P 1 , we need this quadratic to have exactly one real root; so its discriminant must be zero, ie
( 1 − 2 c ) 2 = 4 ( c 2 − r 2 )
Tidying again, this gives
1 − 4 c + 4 r 2 = 0
Putting these equations together, we can express a in terms of r :
a = ( r + 2 1 ) 2
Finally, let A be the area between the two parabolas:
A = 2 ∫ 0 2 1 4 a − 1 a − 4 a − 1 x 2 − x 2 d x = 3 2 a 4 a − 1
The fraction we wish to maximise is A π r 2 .
Since we're after the diameter of the circle, it makes sense to write everything in terms of r ; the area fraction is then
f ( r ) = ( 2 r + 1 ) 2 r ( r + 1 ) 3 π r 2
To find the maximum, set f ′ ( r ) = 0 ; this gives (after some messy differentiation)
f ′ ( r ) = − 2 ( r ( 1 + r ) ) 3 / 2 ( 1 + 2 r ) 3 3 π r 2 ( 4 r 2 − 3 ) = 0
which, when we discount r ≤ 0 becomes the much nicer 4 r 2 − 3 = 0 .
The question asks for the square of the diameter; this is just 4 r 2 = 3 . The fraction of the area between the two parabolas occupied by the circle is around 7 4 . 5 % .