Parabolic Eye
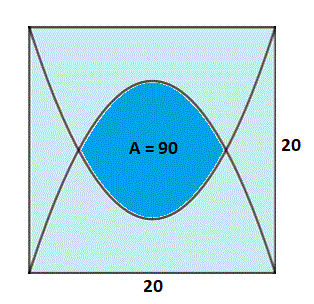 If a
2
0
×
2
0
square is intersected by two symmetrical parabolas so that the parabola opening upward goes through the two upper corners of the square and the parabola opening downward goes through the two lower corners of the square, and the region between the two parabolas has an area of
9
0
, find the distance between the two intersection points of the parabolas.
If a
2
0
×
2
0
square is intersected by two symmetrical parabolas so that the parabola opening upward goes through the two upper corners of the square and the parabola opening downward goes through the two lower corners of the square, and the region between the two parabolas has an area of
9
0
, find the distance between the two intersection points of the parabolas.
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice solution!
Let the vertices of the square be at ( ± 1 0 , ± 1 0 ) , and let the vertex of the parabola opening upward be ( 0 , − k ) .
Then the equation of this parabola (through ( 0 , − k ) , ( − 1 0 , 1 0 ) , and ( 1 0 , 1 0 ) ) is y = 1 0 0 k + 1 0 x 2 − k , which has x -intercepts of x = ± k + 1 1 0 k .
The area of the region between the parabolas is then 4 ⋅ 3 2 ⋅ k ⋅ k + 1 1 0 k = 9 0 , which solves to k = 8 4 5 .
Therefore, the x -intercepts are x = ± 8 4 5 + 1 1 0 8 4 5 = ± 6 , which makes the width of the region between the parabolas 6 + 6 = 1 2 .
Start by defining some coordinates: take the centre of the square as the origin, and define the axes parallel to the sides of the square.
By symmetry in the x -axis, the two intersection points are just the roots of the two parabolas, so we only need to consider one of them (let's choose the upward opening one). Say its equation is y = a ( x 2 − r 2 ) , so that its roots are ± r and the distance between them is 2 r . (Here we've used symmetry in the y -axis.)
We also know it passes through the point ( 1 0 , 1 0 ) , so that 1 0 = a ( 1 0 0 − r 2 ) , or a = 1 0 0 − r 2 1 0 .
We need to find the area of this parabola below the x -axis; this will be 2 A = 4 5 . We can find this by calculus, but this is an excuse to use some Archimedes - eureka! This tells us the area of the parabolic segment will be 3 2 b h , where b is the length of the base and h is the height of the segment.
Clearly b = 2 r ; to find h , put x = 0 into the equation of the parabola, giving h = a r 2 (note we change the sign as the y -intercept of this parabola is below the x -axis).
Putting all this together we get 4 5 = 3 2 × 2 r × 1 0 0 − r 2 1 0 r 2 ; this can be solved by rearranging and factorising to get r = 6 , giving the distance between the intersection points as 1 2 .