Parabolic geometry!
Given below is the graph of a Quadratic polynomial f ( x ) = x 2 − b x + c :
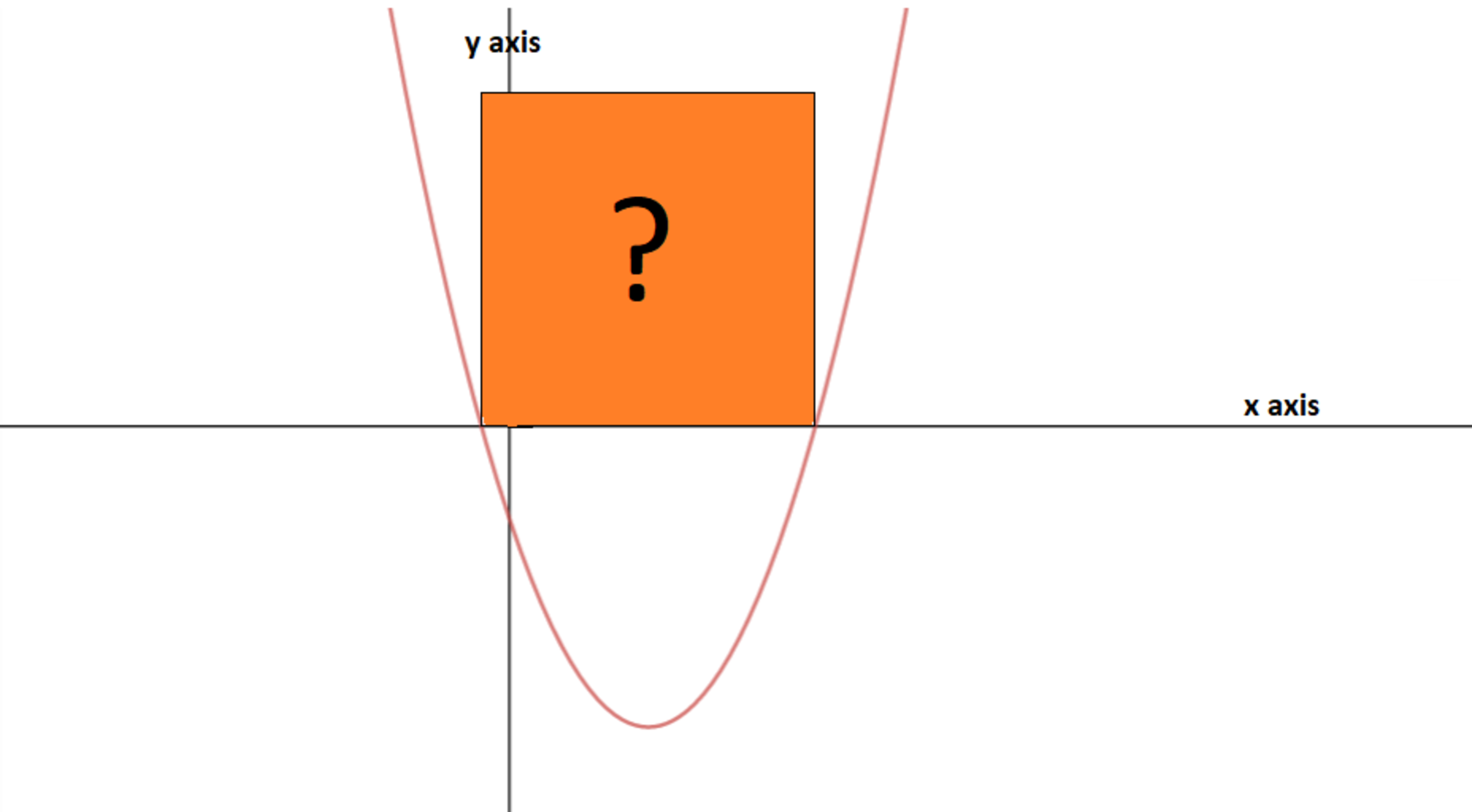
If b 2 − 4 c = 1 5 then what is the area of the orange colored square in the graph?
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
How ( b 2 − 4 c ) 2 = b 2 − 4 c ?
Log in to reply
@Zakir Husain , oopsie big typo
Thanks! Fixed it!
From the quadratic formula, the roots of the polynomial f ( x ) = x 2 − b x + c are found at
x = 2 − b ± b 2 − 4 c ,
Thus, the difference between the roots is 2 − b + b 2 − 4 c − 2 − b − b 2 − 4 c = b 2 − 4 c
This difference is the length of the base of the orange square, thus the area of the square is b 2 − 4 c = 1 5
Area of the orange square=Square of difference of roots = b 2 − 4 c = 1 5
See here to get the above formula
The two roots of the equation x 2 − b x + c are: x 1 = 2 − b − b 2 − 4 c x 2 = 2 − b + b 2 − 4 c
∣ x 1 − x 2 ∣ = 2 − b − 2 ( − b ) + 2 b 2 − 4 c − ( − 2 b 2 − 4 c )
∣ x 1 − x 2 ∣ = b 2 − 4 c
Area = ( ∣ x 1 − x 2 ∣ ) = ( b 2 − 4 c ) 2 = b 2 − 4 c = 1 5