Parabolic Petals
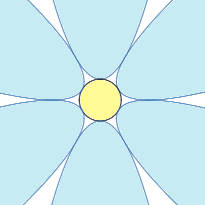
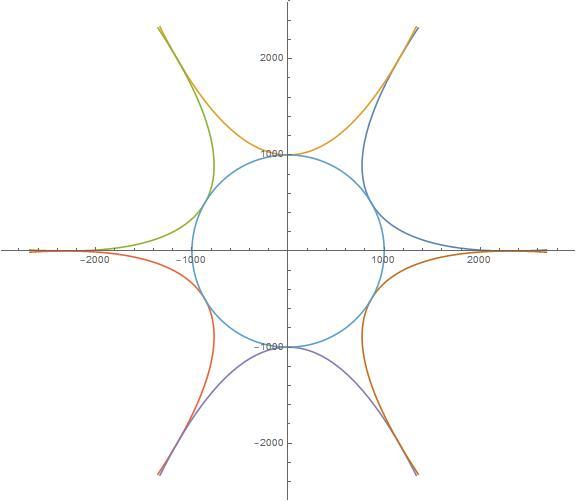
If six congruent parabolas with the formula of y = x 2 are translated and rotated so that each vertex is tangent to a single circle, and each parabola is tangent to its two adjacent parabolas, as shown in the picture, then the radius of the single circle is b a , where a and b are positive co-prime integers.
Find a + b .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Great solution, thanks for posting!
The equation of the parabola with axis as positive Y-axis is y=x^2+r, where r is the radius of the circle. y=x√3 is one tangent to this parabola. Therefore the x-coordinate of the point of contact of this tangent with the parabola is √3/2. The point of contact has the x-coordinate as a solution of the equation x^2-x√3+r=0. Comparing this with the value of x=√3/2, we obtain 3-4r=0 or r=3/4
If we consider any one of the parabola's vertex as origin and its axis as y- axis, the tangent will be at 60° and slope √3 . Lets find its equation by satisfying the common point with parabola The y- intercept of this tangent line is the center of circle. Radius = 3/4
Unfortunately, the radius can be made to be any desired value by changing the scale of the problem. Yes, at some scale, it can be 4 3 . The problem with the problem is that all parabola are the same relative shape. Your problem specification only said that the shape of the parabola was y = x 2 . It did not say that the formula of the parabola exactly was y = x 2 . The later statement sets the problem's scale. The first statement does not.
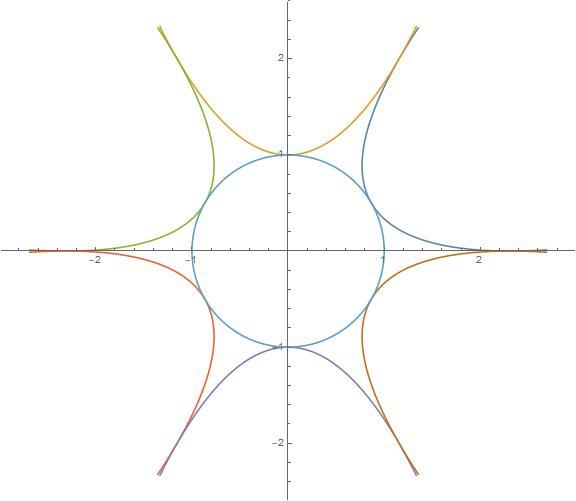
That is why I reported your problem.
unit = 1 ; ParametricPlot [ Evaluate [ Join [ Table [ RotationTransform [ 6 1 ( 2 π ) i ] [ 3 1 ( 4 unit ) { u 2 + 4 3 , u } ] , { i , 2 1 , 2 1 1 } ] , unit ( cos ( π u ) , sin ( π u ) ) ] ] , { u , − 1 , 1 } , ImageSize → Large ]
Finally, I took a chance that you meant, but didn't say, that the formula of the parabola was y = x 2 before rotation and translation and entered that as an answer. Fortunately for me, that worked.
"six congruent parabolas in the form of y = x 2 " means that the equation of each parabola starts out with y = x 2 but then are translated and rotated to make the picture in the problem. This was already explained in my response to your report. As none of the graphs you provided have parabolas in the form of y = x 2 , but rather have parabolas in the form of y = a x 2 for some coefficient other than 1 , they are all incorrect.
And, I say that you were not specific enough. I could not see your response. So, what was your response?
As soon as you brought congruency into the problem you lost your argument about specifying the scale. All parabolas are congruent.
Let the center of the circle be the origin of the x y -plane and its radius be r . Then the equation of the top parabola is y = x 2 + r . We note that the tangent touching two adjacent parabolas passes through the original and they are 6 0 ∘ apart. The tangent in the first quadrant which the top parabola touches is y = x tan 6 0 ∘ = 3 x . Therefore the point where the top parabola touches the parabola on the right satisfies the following system of equation.
{ y = x 2 + r y = 3 x ⟹ x 2 + r = 3 x ⟹ x 2 − 3 x + r = 0 ⟹ x = 2 3 ± 3 − 4 r .
When r is too small, there are two solutions. When r is too big, there is no solution. When the parabola is only touching the tangent the is only one solution. This means that 3 − 4 r = 0 ⟹ r = 4 3 .
Therefore, a + b = 3 + 4 = 7 .