Parabolic Sine Wave Substitute

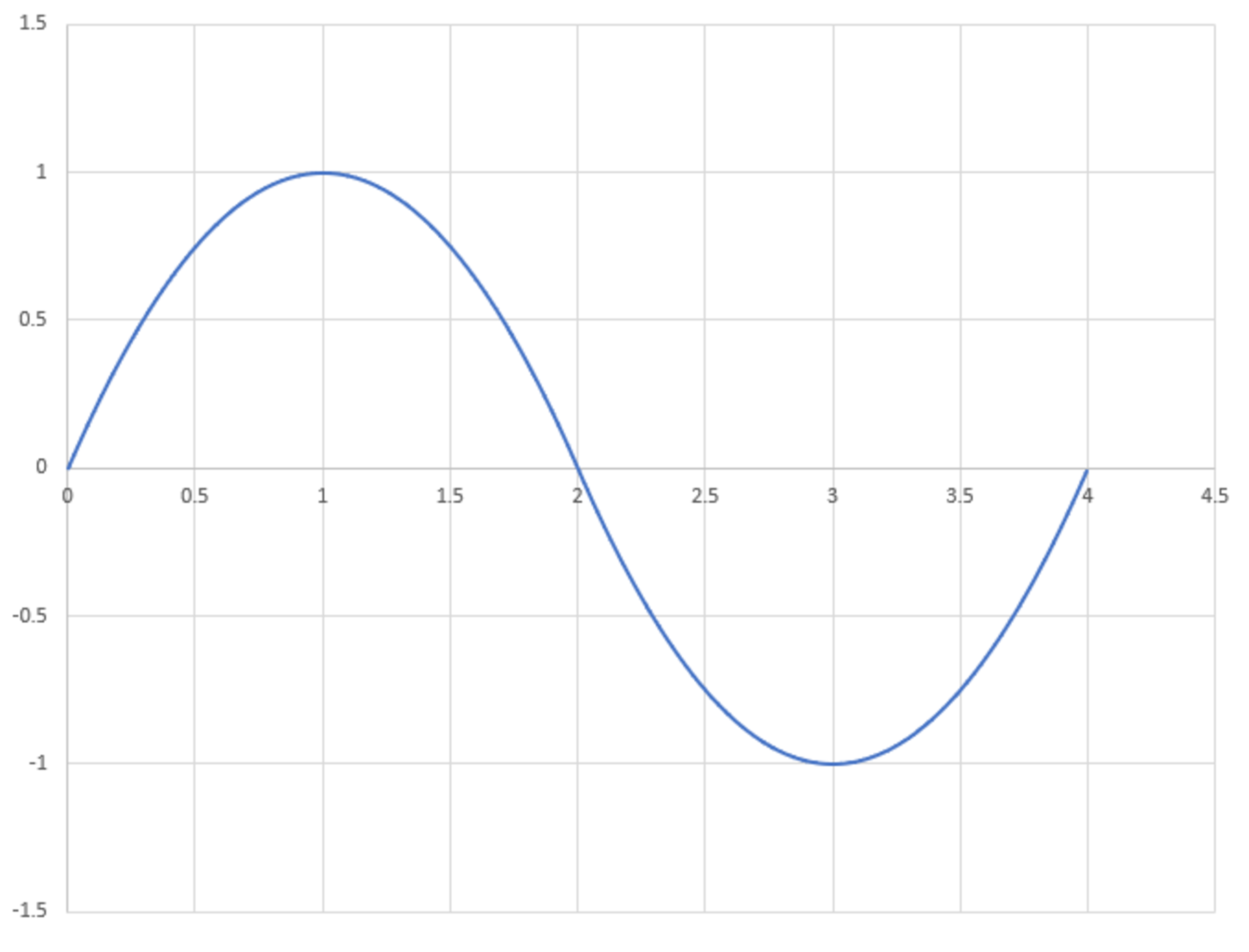
It is common knowledge that for a sine wave, the ratio of the peak value to the root mean square (RMS) value is $\sqrt{2}$ . Suppose we construct a periodic signal resembling a sine wave, composed of parabolic segments placed end to end, with oscillating polarity. Each parabolic segment has the shape of the curve $(y = x^2, -1 \leq x \leq 1)$ (see image).

For this signal, the ratio of the peak value to the RMS value is:

$\frac{\text{Peak}}{\text{RMS}} = \sqrt{\frac{A}{B}}$

If $A$ and $B$ are positive co-prime integers, determine $A + B$ .