Parabolic Triangle
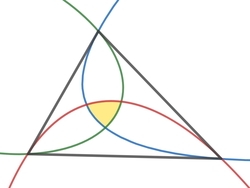 Three parabolas are drawn such that they are tangent to the sides of a triangle at its vertices.
Three parabolas are drawn such that they are tangent to the sides of a triangle at its vertices.
If the area of the triangle is , find the area of the region (shaded in yellow) bounded by the three parabolas.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The triangle can be stretched to a unit equilateral triangle △ P Q R and still preserve the ratio of areas. If the triangle is placed with its center at the origin, the coordinates for P , Q , and R are P ( 0 , 3 3 ) , Q ( 2 1 , − 6 3 ) , and R ( − 2 1 , − 6 3 ) . Also label in A , B , and C as follows:
By symmetry, the red parabola will have an equation of y = a x 2 + b , and its slope will be y ′ = 2 a x . At Q x = 2 1 it has a slope of y ′ = − 3 , so − 3 = 2 a 2 1 , which solves to a = − 3 . Since the red parabola also goes through Q ( 2 1 , − 6 3 ) , we know that − 6 3 = − 3 ( 2 1 ) 2 + b which solves to b = 1 2 3 . Therefore, the equation of the red parabola is y = − 3 x + 1 2 3 , and the coordinates of C are C ( 0 , 1 2 3 ) .
Also by symmetry, A O makes a 3 0 ° angle with the x -axis, so it has a slope of tan 3 0 ° = 3 3 which means it is on the line y = 3 3 x .
Since A is at the intersection of y = − 3 x + 1 2 3 and y = 3 3 x , its coordinates are A ( 6 1 , 1 8 3 ) . The coordinates for B are then B ( 0 , 1 8 3 ) .
The area of △ A B O is A △ A B O = 2 1 ⋅ 6 1 ⋅ 1 8 3 = 2 1 6 3 , and the area of region A B C is A A B C = 3 2 ⋅ 6 1 ⋅ ( 1 2 3 − 1 8 3 ) = 3 2 4 3 .
By symmetry, the area of the shaded region is A shaded = 6 ( A △ A B O + A A B C ) = 6 ( 2 1 6 3 + 3 2 4 3 ) = 1 0 8 5 3 = 2 7 5 ⋅ 4 3 .
Since the area of a unit equilateral triangle is △ = 4 3 , by substitution the area of the shaded region is A shaded = 2 7 5 △ .