Paraboloid Volume
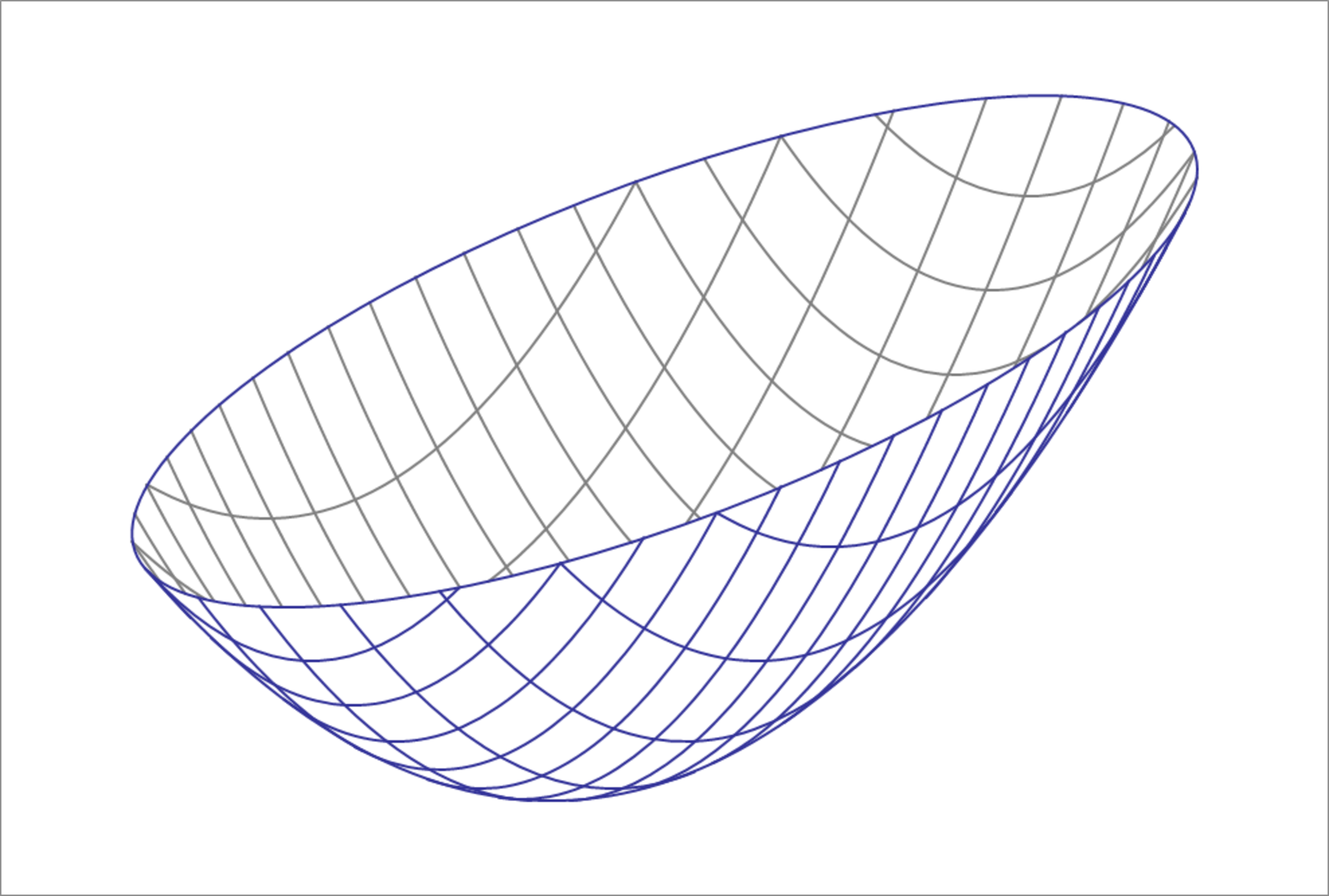
The paraboloid given by the equation above is cut by the plane
Find the volume of the region bounded by the paraboloid and the plane. If the volume can be written as , where are coprime positive integers , enter as your answer.
The answer is 33.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The volume is V = ∬ x 2 + 4 y 2 ≤ x + 4 [ 1 + 4 1 x − ( 4 1 x 2 + y 2 ) ] d x d y = ∬ ( x − 2 1 ) 2 + 4 y 2 ≤ 4 1 7 [ 1 6 1 7 − 4 1 ( x − 2 1 ) 2 − y 2 ] d x d y Parametrizing the region of integration by x = 2 1 + r cos θ y = 2 1 r sin θ 0 ≤ r ≤ 2 1 7 , 0 ≤ θ ≤ 2 π we see that V = 2 1 ∫ 0 2 π d θ ∫ 0 2 1 7 ( 1 6 1 7 − 4 1 r 2 ) r d r = 2 5 6 2 8 9 π making the answer 1 7 + 1 6 = 3 3 .