Parallel conductors
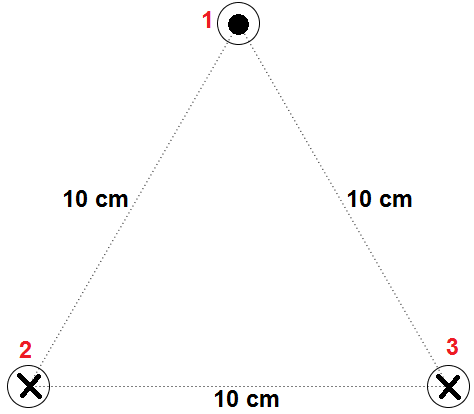
We have three infinite straight conductors carrying current as shown above. Let be the current on the conductor. Find the force per unit length on conductor 3. If , find .
Details and assumptions
- , ,
- , , and are positive integers, is a square-free number, and .
- (a cross) means that the current goes inside the screen, and (a dot) means that the current goes outside the screen.
- is a vector with magnitude and angle with respect to the positive x-axis.
The answer is 219.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
B 1 , 3 = 2 π r 1 , 3 μ 0 I 1 = 2 π ( 0 . 1 m ) ( 4 π × 1 0 − 7 A 2 N ) ( 5 A ) = 1 × 1 0 − 5 T
B 2 , 3 = 2 π r 2 , 3 μ 0 I 2 = 2 π ( 0 . 1 m ) ( 4 π × 1 0 − 7 A 2 N ) ( 1 0 A ) = 2 × 1 0 − 5 T
To determine the directions we use the right hand rule as shown above. By simple geometry we get:
B 1 , 3 ^ = cos 3 0 ∘ i ^ + sin 3 0 ∘ j ^ = 2 3 i ^ + 2 1 j ^
B 2 , 3 ^ = cos 2 7 0 ∘ i ^ + sin 2 7 0 ∘ j ^ = − j ^
Then we find the total magnetic field on conductor 3:
B 3 = B 1 , 3 + B 2 , 3 = 1 × 1 0 − 5 T ( 2 3 i ^ + 2 1 j ^ ) + 2 × 1 0 − 5 T ( − j ^ ) = 2 3 × 1 0 − 5 T i ^ − 2 3 × 1 0 − 5 T j ^
Finally, we find the force per unit length on conductor 3, where l ^ is the direction of the current:
l F 3 = I 3 l ^ × B 3 = ( 2 0 A ) ( − k ^ ) × ( 2 3 × 1 0 − 5 T i ^ − 2 3 × 1 0 − 5 T j ^ ) = − 3 × 1 0 − 4 m N i ^ − 3 × 1 0 − 4 m N j ^
We convert to polar form to get the answer:
l F 3 = 2 3 × 1 0 − 4 m N ∠ 2 1 0 °
Hence a = 2 , b = 3 , c = 4 , θ = 2 1 0 ° and a + b + c + θ = 2 1 9 .