Parallel and perpendicular, part 2

Calculus Level 4

{ x 2 + y 2 = 1 x 2 − 2 x y + 3 y 2 = k \begin{cases} x^2+y^2=1 \\ x^2-2xy+3y^2 =k\end{cases}

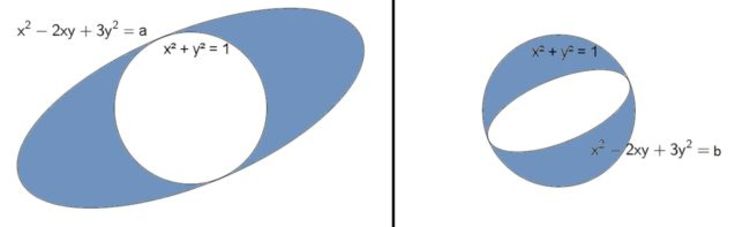
The above two curves touch each other at k = a k=a and k = b k=b where a > b a>b .

Let the area enclosed between the two curve be M M and m m for the case k = a k=a and k = b k=b respecively. Find the value of ⌊ 1000 M m ⌋ \left\lfloor{\dfrac{1000M}{m}}\right\rfloor .


The answer is 2414.

Chan Lye Lee by Chan Lye Lee , 44, Singapore

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Otto Bretscher
Nov 22, 2015

The symmetric matrix of the quadratic form q ( x , y ) = x 2 − 2 x y + 3 y 2 q(x,y)=x^2-2xy+3y^2 is A = [ 1 − 1 − 1 3 ] A=\begin{bmatrix}1&-1\\-1&3\end{bmatrix} and the area of the ellipse q ( x , y ) = k q(x,y)=k is k π det ⁡ A = k π 2 \frac{k\pi}{\sqrt{\det A}}=\frac{k\pi}{\sqrt{2}} . Using the values k = 2 ± 2 k=2\pm \sqrt{2} from the first part , we find M = 2 π , m = ( 2 − 2 ) π M=\sqrt{2}\pi, m=(2-\sqrt{2})\pi and M m = 1 + 2 ≈ 2.414 \frac{M}{m}=1+\sqrt{2}\approx 2.414 . The answer we seek is 2414 \boxed{2414}

1 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

Great! An understanding of quadratic forms and discriminants provide a further understanding that is useful for solving otherwise tedious problems like this.

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...