Parallel Lines?
Geometry
Level
2
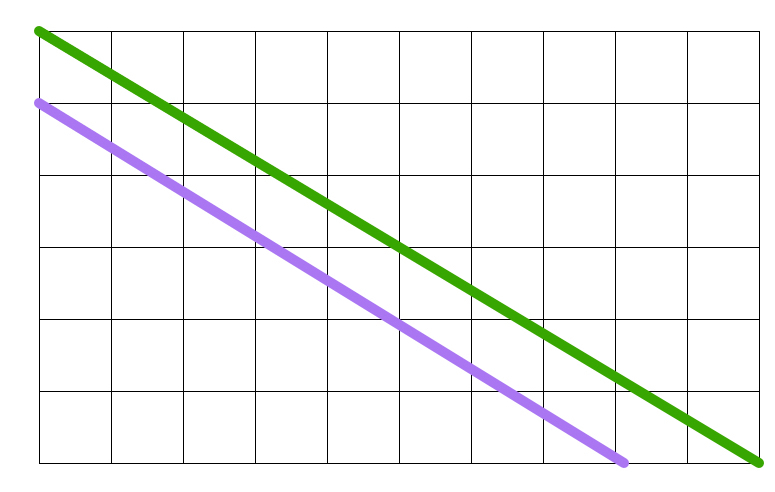
The bold green and purple lines connect up vertices of the grid.
Are they parallel?
No
Yes
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We can calculate the gradients (a.k.a. slopes) of each line by drawing two right angled triangles (one for each line, vertices are the endpoints of the green/purple line and the lower left corner) and dividing the length of the vertical side by the length of the horizontal side:
m g r e e n = 1 0 − 6 = − 0 . 6
m p u r p l e = 8 − 5 = − 0 . 6 2 5
Since the two gradients are not equal, therefore the green and the purple lines are not parallel.
Hence, our answer is:
N o