Parallel lines
The two green lines are parallel. The two red segments are equal and the two purple segments are equal too. The blue angle is
9
0
°
.
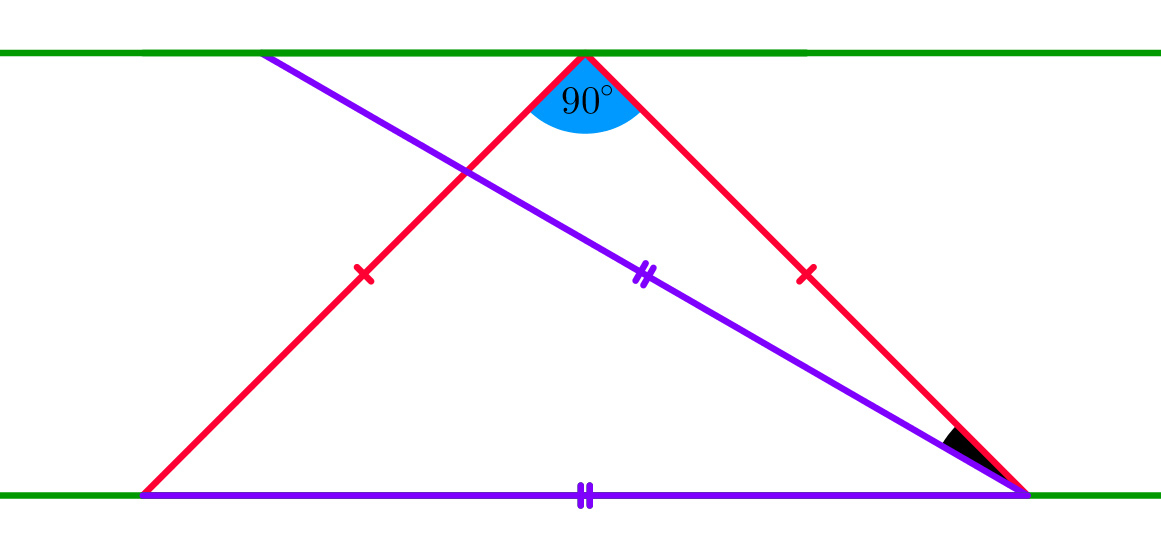
How big is the black angle:
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
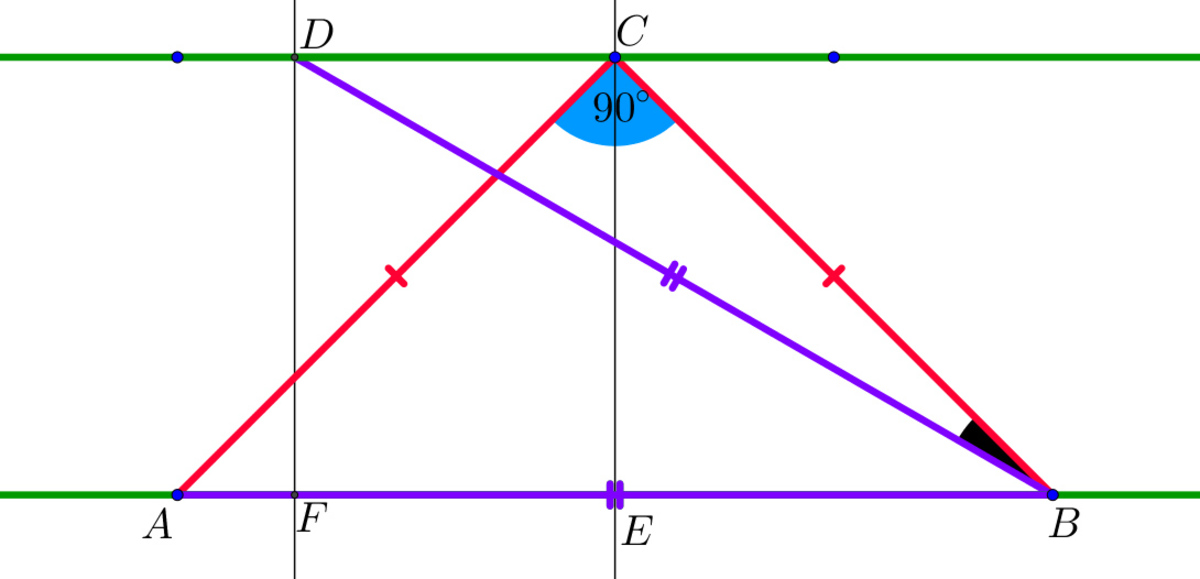
We drop perpendiculars from C and D to A B . The E C D F is a rectangle, so C E = D F . Since ∠ C A B = 4 5 ° , D F = C E = A E = E B . From that D B = A B = 2 ∗ E B and D F = 2 1 D B . Since ∠ D F E = 9 0 ° , ∠ D B F = 3 0 ° . Therefore ∠ C B D = ∠ C B E − ∠ D B F = 4 5 ° − 3 0 ° = 1 5 °
Let A C = C D = 1 . Then by pythagorean theorem , A D = B D = 2 .
Apply cosine law on △ B C D .
( 2 ) 2 = ( B C ) 2 + 1 2 − 2 ( B C ) ( 1 ) ( cos 1 3 5 ) ⟹ ( B C ) 2 + 2 B C − 1 = 0
By the quadratic formula , B C = 2 − 2 + 6
Apply again cosine law on △ B C D .
( 2 − 2 2 + 6 ) 2 = 1 2 + ( 2 ) 2 − 2 ( 1 ) ( 2 ) ( cos x )
After calculation, we get
x = 1 5 ∘