Parallel Resistors
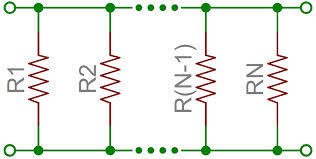 As shown in the figure above,
n
resistors
R
1
,
R
2
,
R
3
,
⋯
,
R
n
each having equal resistance
R
are connected in parallel. Find the effective resistance of the whole network.
As shown in the figure above,
n
resistors
R
1
,
R
2
,
R
3
,
⋯
,
R
n
each having equal resistance
R
are connected in parallel. Find the effective resistance of the whole network.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Discussions for this problem are now closed
As it was given equal resistance let us assume each resistance to be R. Now let us consider only 2 resistors in parallel we get (R.R)/(R+R)= R/2 As we did for 2 resistors denominator was 2, if we do for n no: of resistors we get R/n
effectiive resistance=R/n hence R(sum of the resistance) and n(number of resistors).
Effective resistance:
1/Reff = 1/R1 + 1/R2+......+ 1/Rn
since equal resistance R1=R2=........=Rn
1/Reff = 1/R+1/R+......+1/R
1/Reff = n/R
or Reff = R/n
Make it like this:
The formula is:
R 1 1 + R 2 1 ... + R ( N − 1 ) 1 R N 1
Because of R1=R2=R(N-1)=RN so we make all R(1,2,...,N} to be R:
R 1 + R 1 + R 1 + R 1 + ..... = R n
n= ∑ 1
Then do the magic:
R n 1 = n R
When n resistors are connected in parallel, the equivalent resistance \(R_{eq}is given by:
\[\frac{1}{R_{eq}}=\sum _{ i=1 }^{ n }{ \frac { 1 }{ { R }_{ i } } } \]
For n resistors of equal resistance R , we have:
R e q 1 = R n ⇒ R e q = n R