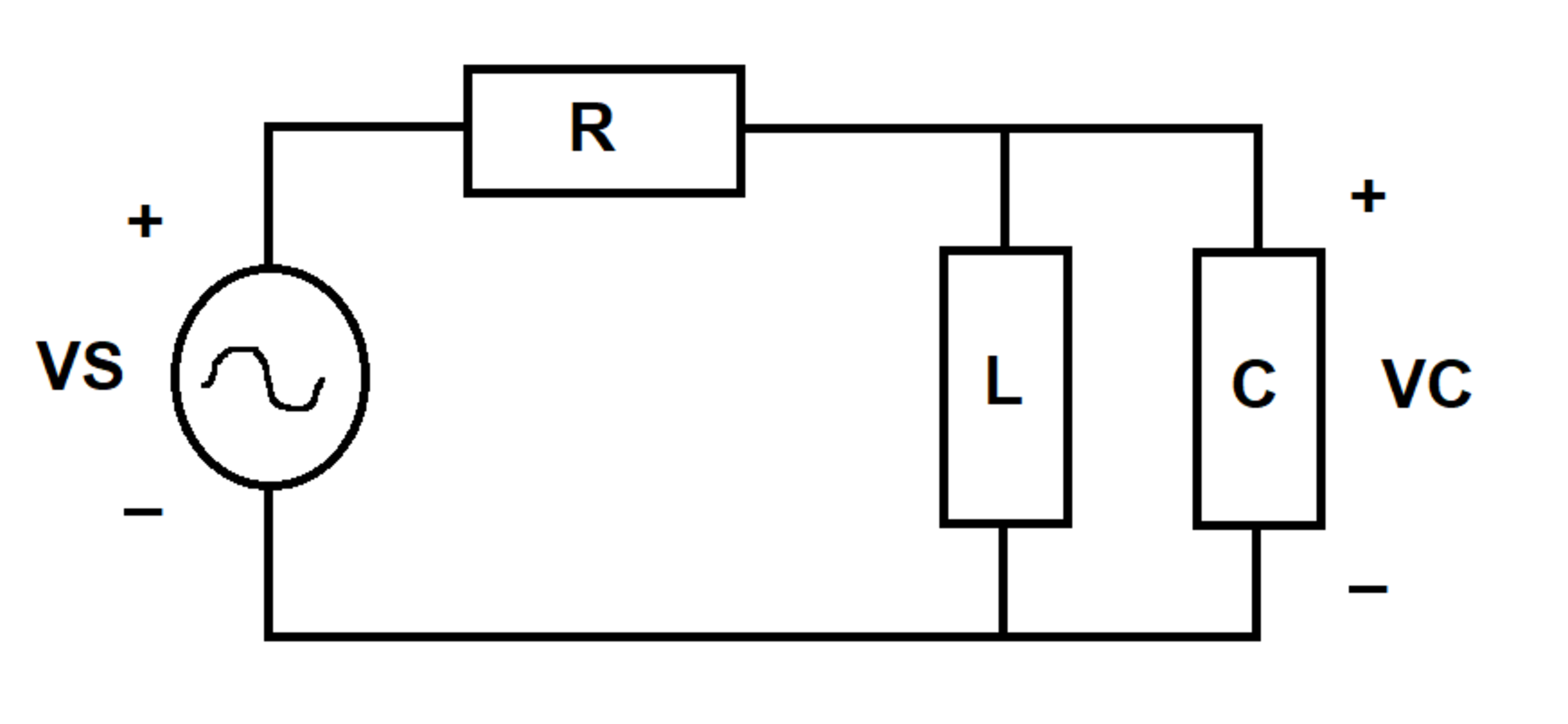
Parallel Resonance

Current through the resistor is $I_R$ , through the inductor is $I_L$ and through the capacitor is $I_C$ . Charge on the capacitor is $Q$ . CIrcuit equations:

$I_R + \dot{I}_L = \sin{t}$ $I_R =I_L+I_C$ $\dot{I}_L = Q$ $\dot{Q} = I_C$ $V_C = Q$

Converting all equations to Laplace domain and solving for $V_C(s)$ gives:

$V_C(s) = \frac{s}{(s^2+1)(s^2+s+1)}$

Inverse Laplace transform (steps left out) gives:

$V_C(t) = \sin{t} - \frac{2\mathrm{e}^{-t/2}}{\sqrt{3}} \sin\left(\frac{t\sqrt{3}}{2}\right)\implies V_S(t) - V_C(t) = \frac{2\mathrm{e}^{-t/2}}{\sqrt{3}} \sin\left(\frac{t\sqrt{3}}{2}\right)$

$\implies \int_{0}^{\infty} \frac{2\mathrm{e}^{-t/2}}{\sqrt{3}} \sin\left(\frac{t\sqrt{3}}{2}\right) \, dt = \boxed{1}$