Parallel, serial or something else?
Estimate the total electrical resistance of the network shown below in units of .
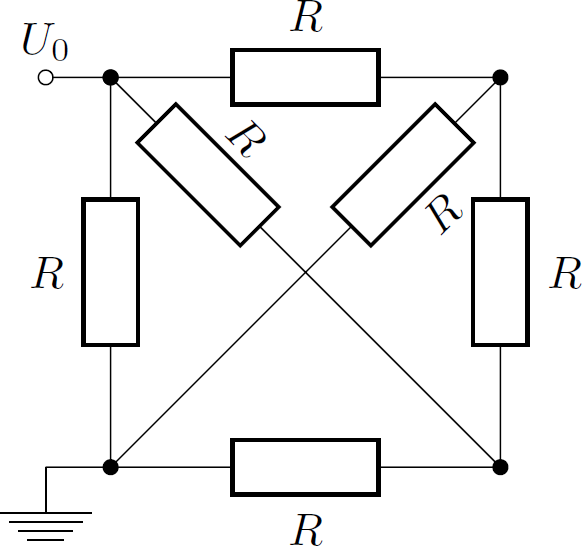
Hint: Connection nodes are indicated by the dots. The intersecting diagonals are not directly connected.
The answer is 0.500.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The whole network consists of four fully connected knots, which are labeled with an index i = 0 , 1 , 2 , 3 .
Each knot has a corresponding electric potential U 0 , U 1 , U 2 and U 3 = 0 (ground)
The current I i j between two knots follows Ohm's law I i j = R U i − U j
For the points i = 1 and 2 Kirchhoff's current law states I 1 0 + I 1 2 + I 1 3 I 2 0 + I 2 1 + I 2 3 = R U 1 − U 0 + R U 1 − U 2 + R U 1 = R 1 ( 3 U 1 − U 0 − U 2 ) = 0 = R U 2 − U 0 + R U 2 − U 1 + R U 2 = R 1 ( 3 U 2 − U 0 − U 1 ) = 0 This is a linear equation system ( 3 − 1 − 1 3 ) ( U 1 U 2 ) = ( U 0 U 0 ) for the two unknown U 1 , U 2 with the solution U 1 = U 2 = 2 1 U 0
For the point i = 0 the sum of all outgoing currents corresponds to the total current I tot = I 0 1 + I 0 2 + I 0 3 = 2 R U 0 + 2 R U 0 + R U 0 = R 2 U 0
The quotient of total voltage and current yields the total resistance R tot = I tot U 0 = 2 R