Parallel to x-axis
Find the distance between the two horizontal tangents to the curve y = x 3 + x 2 − x .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Nice solution. Thanks! :)
FIRST UP,DIFFERENTIATE Y=F(X) W.R.T X NOW WE GET DY/DX = 3X^2 +2X-1 GIVEN SLOPE=0 THEREFORE, 3X^2+2X-1=0 WE GET X=1/3 , -1 NOW PUTTING X IN THE EQUATION WE GET Y= -5/27 , 1 HORIZONTAL LINE IS OF THE FORM Y=K FROM CALCULATED VALUES WE FIND DISTANCE = 1-(-5/27) = 32/27
This problem does not require Calculus to solve:
Let f ( x ) = x 3 + x 2 − x . Let y = d be the horizontal line tangent to the curve. Then, f ( x ) = d so x 3 + x 2 − x − d = 0 . Since, when graphed, f ( x ) will be tangent to y = d at 2 distinct values of d , there are 2 distinct solutions for f ( x ) = d . Thus, x 3 + x 2 − x − d = 0 has 2 distinct solutions.
Let ( x + b ) ( x + a ) 2 = x 3 + ( 2 a + b ) x 2 + ( a 2 + 2 a b ) x + ( a 2 b ) represent f ( x ) − d = 0 . Then, ( 2 a + b ) = 1 and ( a 2 + 2 a b ) = − 1 . By substitution, simplification, and the Quadratic Formula, ( a , b ) = ( 1 , − 1 ) and ( a , b ) = ( − 0 . 3 3 3 , 1 . 6 6 6 7 ) are obtained. Since d = a 2 b = − 5 / 2 7 and d = 1 are the vertical positions of the horizontal lines. Thus, 1 − ( − 5 / 7 ) = 3 2 / 2 7 which is the final answer.
Given, y = x 3 + x 2 − x For tangents to be horizontal, slope of tangents = 0 ∴ d x d y = 3 x 2 + 2 x − 1 = 0 Solving gives x = − 1 and x = 3 1
Corresponding y values are y = 1 and y = 2 7 − 5 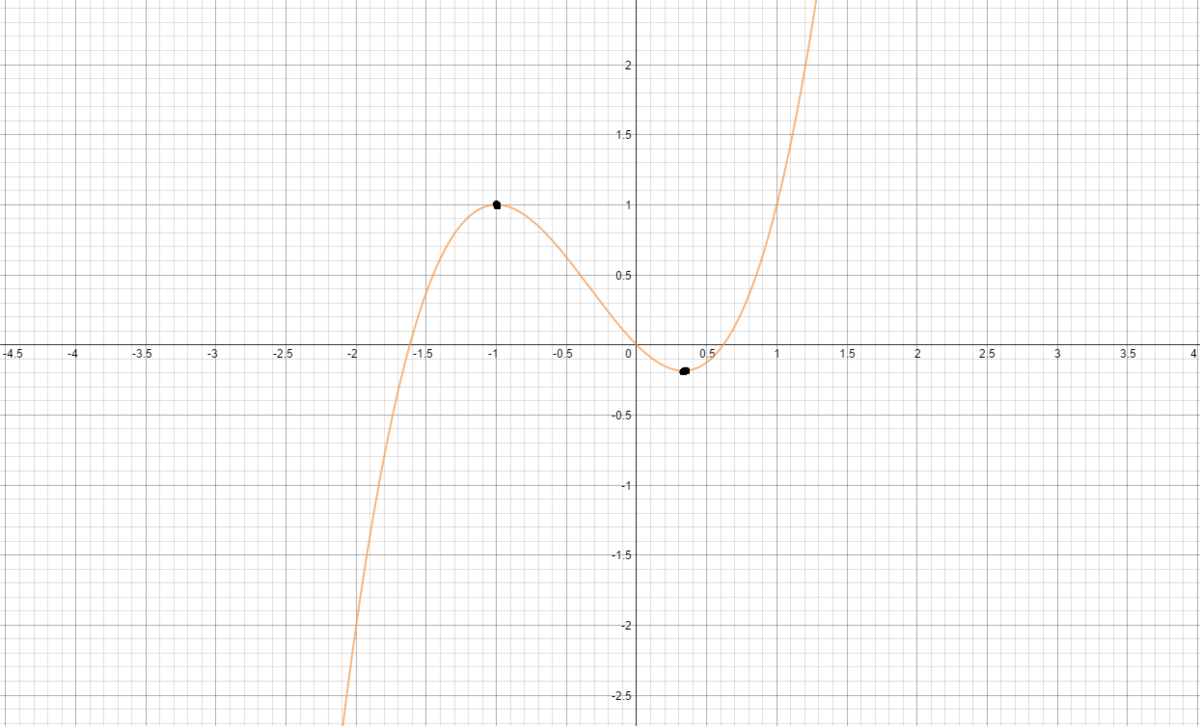
So it is clear that distance between two tangents is [ 1 − 2 7 − 5 ] = 2 7 3 2