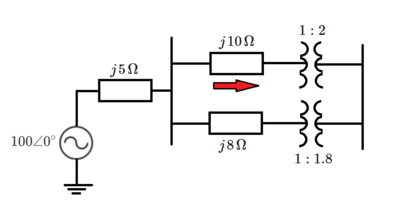
Paralleled Transformers

Electricity and Magnetism Level 5

An AC voltage source feeds a bus through a set of paralleled step-up transformers, as shown in the diagram. The transformers are modeled as impedances in series with ideal transformer windings, with turns ratios as indicated. The source impedance is also shown.

Even though the high-side bus is unloaded (open), the transformers draw current because they have uneven turns ratios and impedances.

What is the magnitude of the current flowing through the $j \, 10 \, \Omega$ impedance?

The answer is 0.60496.

1 solution

Max Yuen
May 4, 2019

The easiest way to solve this problem is to turn the two transformers into a single lumped element with well defined voltage and current ratios.

Another way to see it is to think of the $1:2$ and $1:1.8$ transformers are transformers feeding into each other, so that you get a turns ratio of $1:2$ to $1.8 : 1$ or a turns ratio of $1.8 : 2$ . If we denote the voltage at the primary side for the $1:2$ as $V_1$ and the voltage of the primary side for the $1:1.8$ as $V_2$ , we have $V_1:V_2 = 1.8:2$ or $9:10$ .

Since ideal transformers are energy conserving (doesn't give you more or less power than you put in) the current ratios must be the reciprocal of the turns ratios so $I_1:I_2$ = $10:9$ . There is a phasing issue to remember too, so current in at primary side at the top comes out at primary side at the bottom transformer (flowing back to the $j8\Omega$ towards the source).

Now, we just apply the KVL and KCL rules to solve the rest of the circuit.

Let's use KCL first. To make things simpler, just call the current $I_1 = \frac{10}{9j}I$ and $I_2 =-\frac{1}{j}I$ so the source current is just $\frac{1}{9j}I$ . The complex part is just to make the calculation easier since all impedances are imaginary.

Now, apply KVL to the branches, ending with $V_1$ and $V_2$ , and noting that $V_1 = \frac{9}{10} V_2$ .

(1) top branch $100 - (j5)(\frac{1}{j9})I-(j10)(\frac{10}{9j})I-V_1=0$

(2) bottom branch $100-(j5)(\frac{1}{j9})I+(j8)(\frac{1}{j})I-V_2=0$ <- replace $V_2$ with $\frac{10}{9}V1$

After some rearranging we get

(1) $105 I +9V_1 = 900$

(2) $67I -10V_1 = -900$

$I = \frac{(900)(10)-(900)(9)}{(105)(10)+(67)(9)} = \frac{900}{1653}$

And we also obtain $I_1$ as $\frac{10}{9}I=\frac{1000}{1653}\approx 0.60496$

Nice job, thanks. I had previously been disappointed that nobody solved this one.

Steven Chase - 2 years, 1 month ago

i've two doubts please address if you have time . (i)what is "phasing issue "? and why same current will come back through 8j ohm as is going in through primary (it happens in two port networks but here i can't understand your reasoning please elaborate a bit)

(ii) how do you got I1=(10/9j)I.

rest of your explanation is superb specially lumping of two transformers

veeresh pandey - 2 years ago

i) The phasing issue is due to the way the transformers work. There's always a "phase dot" that indicates if the potential is + at the "dot" and current is going into that terminal, it will also be + at the secondary, but the current flows out at the "dot" side. So you can see that the way the transformers are put together that when a current is flowing along both branches into the primaries, the secondaries should output two currents into the load. Since there is NO load, the current from one secondary back flows into the other secondary and induces a current back in the primary. That flows backwards into the j8 ohm impedance. This is "circulating current" and wastes a lot of energy if there are resistances along the way.

ii) I just found it convenient to express the currents this way, in order to have a current ratio of 10 : 9, as constrained by the turns ratios. (The negative sign is needed too to show the current is flowing back towards the source.)

Max Yuen - 2 years ago

Paralleled Transformers

The answer is 0.60496.

1 solution

0 pending reports