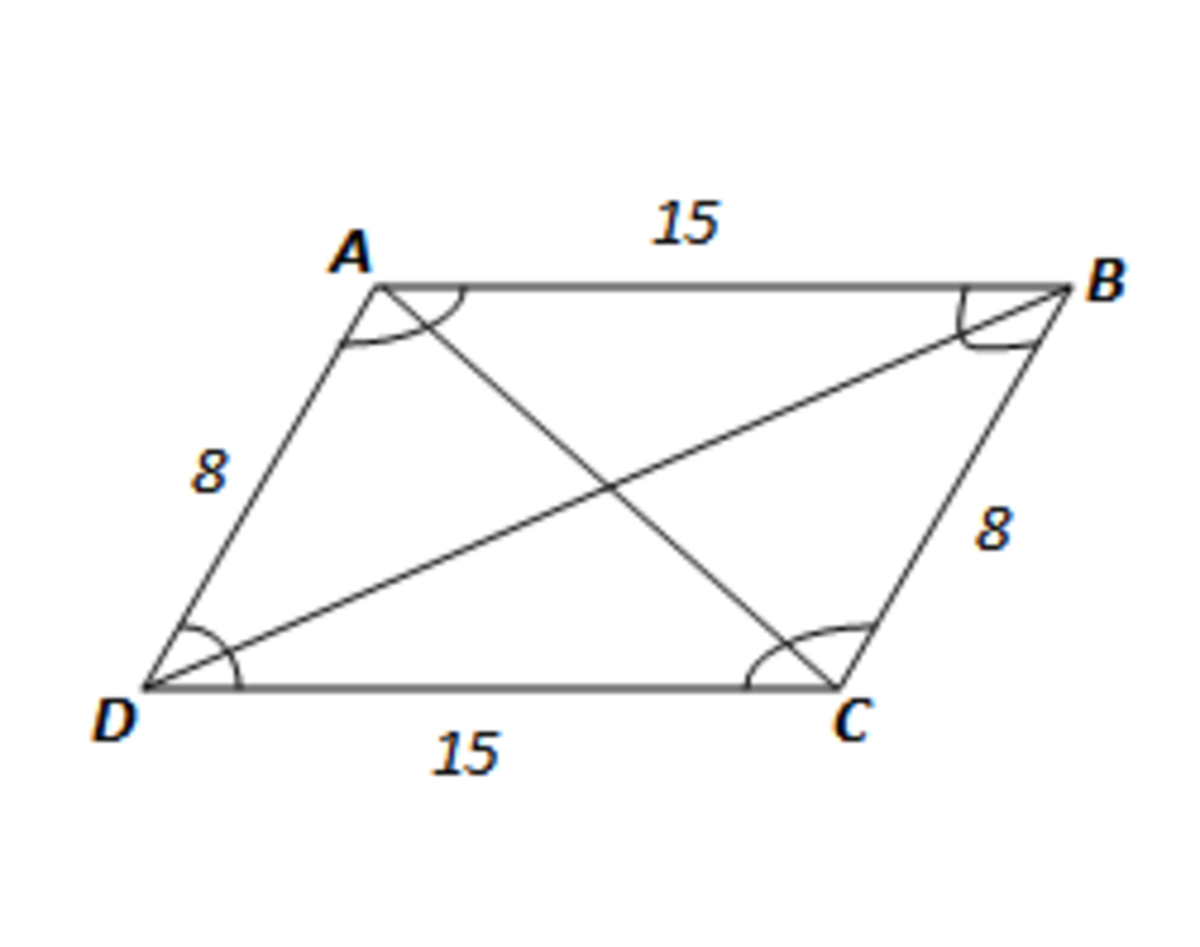
Parallelogram and its diagonal

Let $\angle ADC = \angle ABC = \theta$ , then $\angle DAB = \angle BCD = 180^\circ - \theta$ . By cosine rules,

$\begin{aligned} {\color{#3D99F6}AC^2}+{\color{#D61F06}BD^2} & = {\color{#3D99F6}AD^2+DC^2-2AD\cdot DC \cos (\angle ADC)} + {\color{#D61F06}AD^2+AB^2-2AD\cdot AB \cos (\angle DAB)} \\ & = 8^2+15^2-2\cdot 8\cdot 15 \cos \theta + 8^2 + 15^2 {\color{#D61F06}-} 2\cdot 8\cdot 15 {\color{#D61F06} \cos (180^\circ - \theta)} & \small \color{#D61F06} \text{As }\cos (180^\circ - \theta) = - \cos \theta \\ & = 8^2+15^2-2\cdot 8\cdot 15 \cos \theta + 8^2 + 15^2 {\color{#D61F06}+} 2\cdot 8\cdot 15 {\color{#D61F06} \cos \theta} \\ & = 8^2+15^2 + 8^2 + 15^2 \\ & = \boxed{578} \end{aligned}$

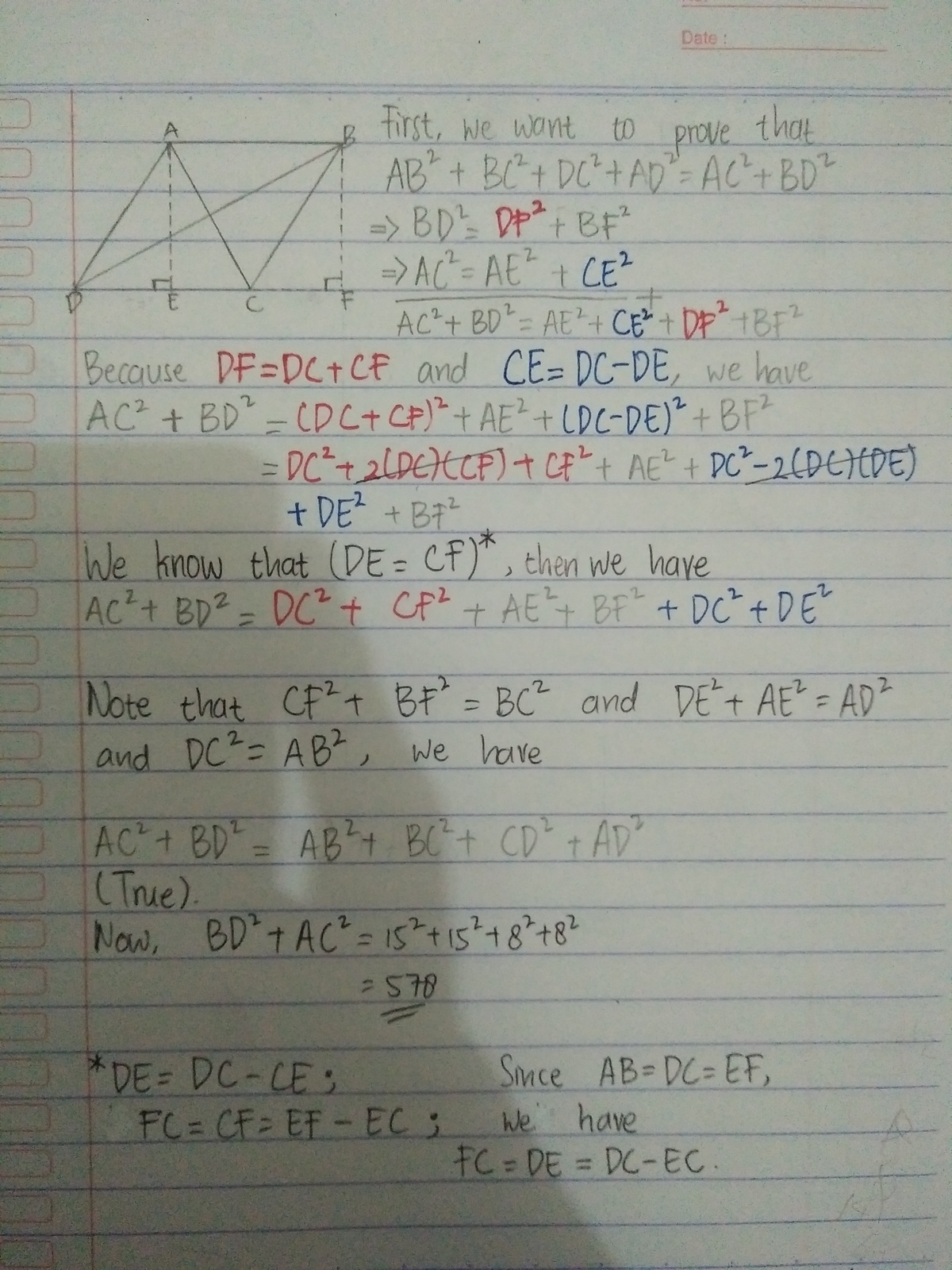
Actually, this problem is very easy, if you already know this proof. And I already knew this proof, so I shared this proof, to make this problem easier.

Using the cosine law:

( DB )^2 = (15)^2 + (8)^2 +2(15)(8) cos C ( AC )^2 = (15)^2 + (8)^2 +2(15)(8) cos D

Also, take note that consecutive angles in a parallelogram are supplementary.

( DB )^2 = 289+240 cos C ( AC )^2 = 289+240 cos D ( AC )^2 = 289+240 cos(180 - C ) ( AC )^2 = 289+240 (-cos C ) ( AC )^2 = 289-240 cos C ( DB )^2 + ( AC )^2 = 289 + 240 cos C + 289 - 240 cos C =578

For this question to work the answer must be independent of the angle between adjacent sides. Thus the answer is the same for a rectangle 2 x (15² + 8²) = 578, or the degenerate line case of (15-8)² + (15+8)² = 578. So the answer is 578.

According to the parallelogram law, the sum of the squares of the lengths of the four sides of a parallelogram equals the sum of the squares of the lengths of the two diagonals. So the desired answer is $2(8^2)+2(15^2) = 578$ .

Just using specializations, the rectangle is also parallelogram.and as you like, 578 is the answer.

Let $x$ = shorter diagonal and $y$ = longer diagonal

By applying cosine law in my figure, we have

$x^2=8^2+15^2-2(8)(15)(cos$ $A) = 289-240cos$ $A$

Similarly,

$y^2=8^2+15^2-2(8)(15)(cos$ $B) = 289-240cos$ $B$

Now we add the squares of the two diagonals,

$x^2+y^2=578-240cos$ $A-240cos$ $B = 578 - 240(cos A + cosB)$

The sum of $<A$ and $<B$ is $180$ , so $cos A$ + $cos B = 0$ .

Thus, we have

$x^2+y^2 = 578$

2 x (15² + 8²) = 578 = d^2 + d^2

Draw a line from B to DC perpendicularly, intersects DC at E, and the length of this line is b. Draw also from C to AB.Let CE=a. Pythagoras : a^2 + b^2 = 8^2 ... (1),
(15+a)^2 + b^2 = BD^2 ... (2),
(15-a)^2 + b^2 = AC^2 .....(3), (2) + (3), and by replacing a^2 + b^2 = 8^2 , we have 2(15^2 + 8^2) = BD^2 + AC^2 . So the sum of the squares of the diagonals of the parallelogram = 578