Parallelogram inscribed in an ellipse
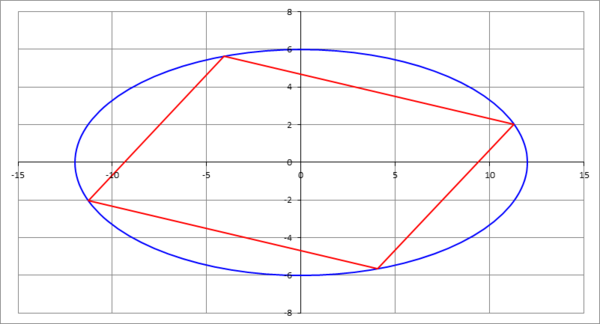
The ellipse shown in the above figure has a semi-major axis length of , and a semi-minor axis length of .
A parallelogram having the angle between two of its adjacent sides equal to as well as having the maximum possible area is inscribed in the ellipse. Find the length of the longer side of the parallelogram. If this length is , enter .
The answer is 15777666.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Start with a square with vertices ( 0 , 0 ) , ( 1 , 0 ) , ( 1 , 1 ) , ( 0 , 1 ) . We want to transform the square into a parallelogram with sides a and b , with a > b and also the angle between the sides is 6 0 ∘ .
For this we use the transformation:
T = [ a 0 b cos 6 0 ∘ b sin 6 0 ∘ ]
Now the minimum area ellipse passing through the vertices of the square we started with is a circle with center C ′ = ( 2 1 , 2 1 ) and radius 2 2 , so its equation is
( r ′ − C ′ ) T ( r ′ − C ′ ) = 2 1
Now we apply the transformation to the circle, and for proper selection of a and b , this should gives us an ellipse with semi-axes 1 2 and 6 . Note that the ellipse generated has the minimum possible area for the resulting parallelogram, which is equivalent to saying the parallelogram has the the maximum possible area for the ellipse.
If r is the transformed point, then r = T r ′ and this implies that r ′ = T − 1 r . Substitute this into the equation of the circle, and this gives you the equation of the ellipse:
( T − 1 r − C ′ ) T ( T − 1 r − C ′ ) = 2 1
which, after simple manipulation, becomes
( r − T C ′ ) t ( 2 T − t T − 1 ) ( r − T C ′ ) = 1
We want to find a , b such the eigenvalues of ( 2 T − t T − 1 ) are the reciprocals of 1 2 2 and 6 2 ; or , such that the eigenvalues of ( 2 T − t T − 1 ) − 1 are 1 2 2 and 6 2
So,
Q = ( 2 T − t T − 1 ) − 1 = 2 1 T T t
hence,
Q = 2 1 [ a 0 b cos 6 0 ∘ b sin 6 0 ∘ ] [ a b cos 6 0 ∘ 0 b sin 6 0 ∘ ]
multiplying out and substituting the values of cos 6 0 ∘ and sin 6 0 ∘
Q = 2 1 ⎣ ⎢ ⎡ a 2 + 4 b 2 b 2 4 3 b 2 4 3 b 2 4 3 ⎦ ⎥ ⎤
The trace of this matrix is the sum of its eigenvalues , and its determinant is the product of its eigenvalues
hence, we want to have
2 1 ( a 2 + b 2 ) = 1 2 2 + 6 2
and
4 1 ( ( a 2 + 4 b 2 ) ( 4 3 b 2 ) − b 4 ( 1 6 3 ) ) = ( 1 2 2 ) ( 6 2 )
which simplifies nicely to
1 6 3 a 2 b 2 = ( 1 2 2 ) ( 6 2 )
Let u = a 2 , v = b 2 , then
u + v = 2 ( 1 4 4 + 3 6 ) = 2 ( 1 8 0 ) = 3 6 0
and u v = ( 1 4 4 ) ( 3 6 ) ( 1 6 ) / 3 = 2 7 6 4 8
from the first of these two equations,
v = 3 6 0 − u
substitute this into the second equation
u ( 3 6 0 − u ) = 2 7 6 4 8
or u 2 − 3 6 0 u + 2 7 6 4 8 = 0
hence
u = 2 1 ( 3 6 0 + 3 6 0 2 − 4 ( 2 7 6 4 8 ) ) = 2 4 8 . 9 3 4 7 5 1 7 5 8 4 5 6 3 4 3
hence a = u = 1 5 . 7 7 7 6 6 6 2 3 2 9 5 2 7 1 5
thus, the answer is 1 5 7 7 7 6 6 6