Parallelogram inside Triangle!
Given a acute angled triangle A B C with sides a = 1 0 , b = 1 1 , c = 1 2 . D , E , F are interior points of the sides B C , C A , A B respectively so that A F D E is a parallelogram. Let the maximum area of the parallelogram be X .
Then ⌊ 1 0 0 X ⌋ is -
a , b , c are standard notations denoting sides of triangle.
The answer is 2576.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
This is basically Ruslan's solution LaTeX-ified. I used a slightly different approach using vectors. (Although it is essentially the same thing.)
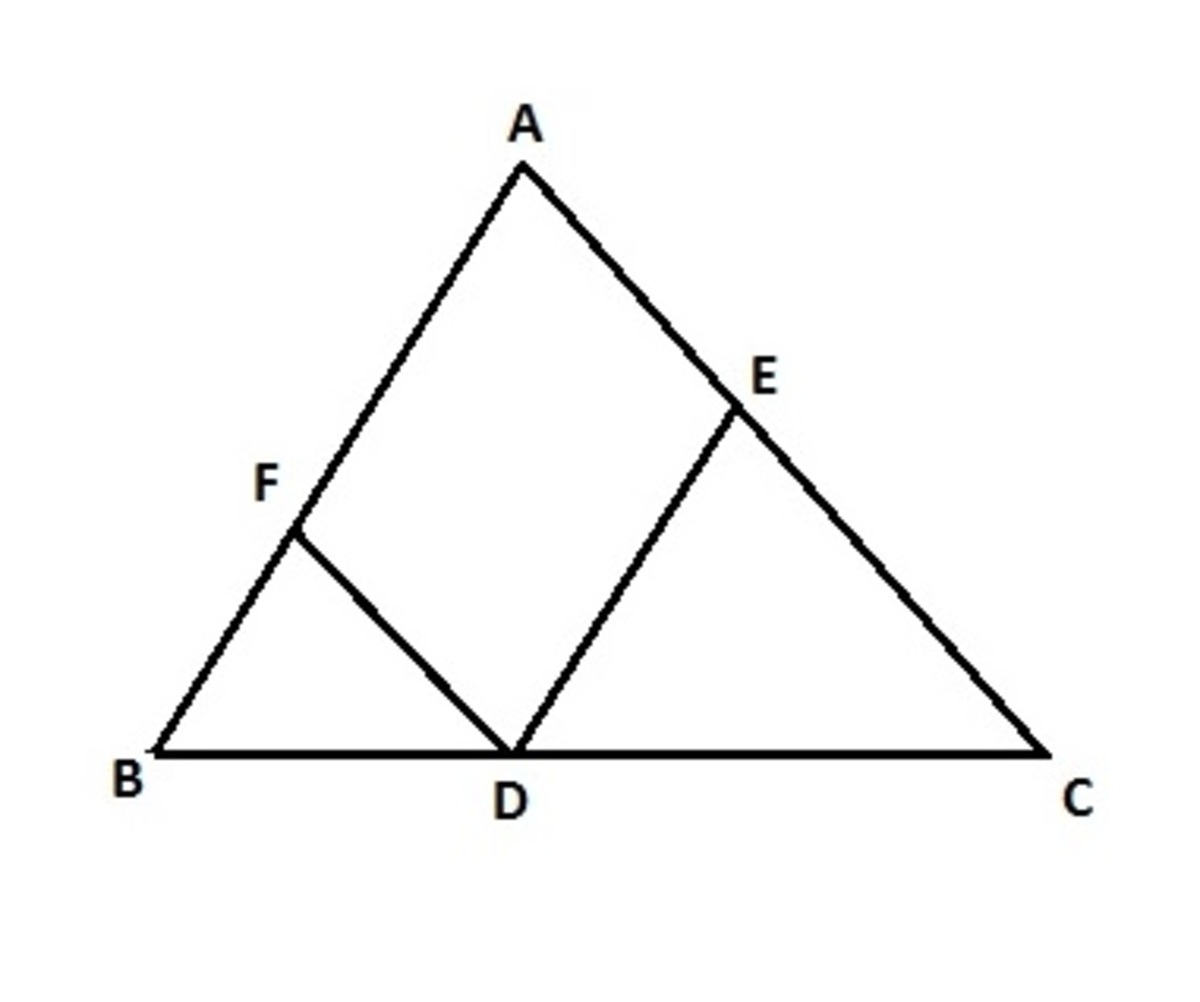
Δ A F D E = Δ A B C − Δ F B D − Δ E D C .
Also, F B D ∼ A B C and E D C ∼ A B C
If F B = x ⇒ Δ F B D = ( c x ) 2 A
A F = c − x ⇒ D E = c − x ⇒ Δ E D C = ( c c − x ) 2 A
Finally, Δ A F D E = Δ A ( 1 − ( c x ) 2 − ( c c − x ) 2 )
Differentiating wrt x we find that the expression attains maxima at x = 2 c .
Substituting in the equation gives the answer Δ A F D E = 2 1 Δ A
Δ A = s ( s − a ) ( s − b ) ( s − c ) and on substiting values comes out to be 5 5 . 1 2 1 2
Therefore, maximum Δ A F D E = 2 7 . 5 6 0 6
Area of triangle ABC = √((16.5)(6.5)(5.5)(4.5) = A, x = [ABC] – [FBD] – [EDC]. [FBD] ,[EDC] are both similar to [ABC]. Let the length of FB = z. Then by similarity
[FBD]=(z/12)2A, and [EDC]=((12 – z)/12)2A, so that z =A - (z/12)2A - ((12 – z)/12)2A = A(- z2/72 + 1/6 z), The stationary value of z (max.of X), dx/dz = A (-z/36 +1/6) = 0, then z=6. So xmax = ½ A = 25.7606. So└ 100x ┘ = 2576.