Parallelogram Riddle II
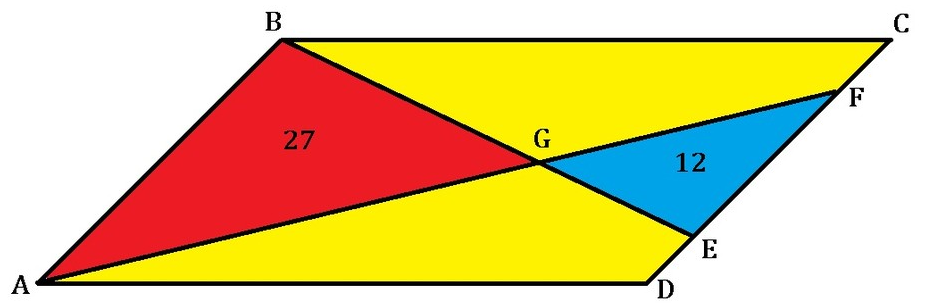
As shown above, a parallelogram A B C D is partitioned by two lines A F and B E , such that the areas of the red △ A B G = 2 7 and the blue △ E F G = 1 2 .
What is the area of the yellow region?
Note : Figure not drawn to scale.
The answer is 51.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
L e t s t . l i n e H G I ∣ ∣ A B . Δ A B G a n d ∣ ∣ g r a m A B H I h a v e t h e s a m e b a s e a n d h e i g h t , ∴ ∣ ∣ g r a m A B H I , a r e a = 2 ∗ 2 7 = 5 4 . R e d a n d b l u e Δ s a r e s i m i l a r , s o B G : G D : : 2 7 : 1 2 = 3 : 2 . ∴ B H : H C : : B G : G D = 3 : 2 . ⟹ a r e a ∣ ∣ g r a m H I D C = 5 4 ∗ 2 / 3 = 3 6 . ∴ y e l l o w a r e a = 5 4 + 3 6 − 2 7 − 1 2 = 5 1 .
My solution is similar to Worranat's , but not identical.
We can shear this parallelogram horizontally into a rectangle without changing areas (by Cavalieri's principle). Thus we may assume that A B C D is indeed a rectangle, which makes everything a bit easier to think through. Since the area of the similar triangles A B G and E F H are in a proportion of 9 : 4 , the linear dimensions are in a proportion of 3 : 2 . In particular, if h is the height of triangle A B G over the side A B , then h + 3 2 h = A D so h = 5 3 ( A D ) . The area of triangle A B C is 2 7 = 2 h ( A B ) = 1 0 3 ( A D ) ( A B ) so that the area of the whole rectangle is ( A D ) ( A B ) = 9 0 . The area of the yellow region is 9 0 − 2 7 − 1 2 = 5 1 .
that's a wrong formula as in the above question we are talking about the parallelogram and not a rectangle
and formula of the area of parallelogram is not side into side instead its base into height
We have 2 similar triangles the red and blue ones, with ratio of sides = √27/√12 = 3/2. So AB=3x,EF=2x,BH=3y,CH=2y. And the area of ΔABG=27 = (3x)(3y)/2,then xy=6. The area of yellow region = 15xy – 39 = 51.
If you are in a rush cheat by using a rectangle and have BA=3 EF=2 and find out AD=30 and do 30*3-39.
As alternate interior angles of parallel lines, ∠ A B G ≅ ∠ F E G and ∠ B A G ≅ ∠ E F G , so △ A B G ∼ △ F E G by AA similarity. Therefore, we can extend G E to the same length of G B to H and extend G F to the same length of G A to I to create parallelogram A B I H with the same height of parallelogram A B C D . Let J K and J L be the midsegments of parallelograms A B C D and A B I H , respectively.
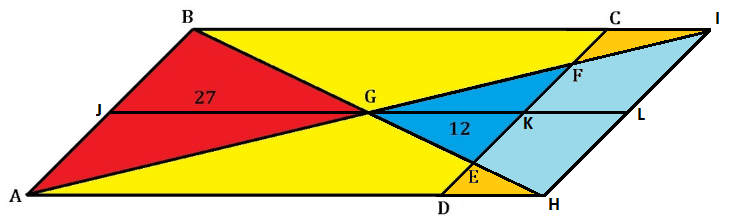
The ratio of the sides of the △ F E G to △ A B G is the square root of the ratio of their areas, which is 2 7 1 2 = 3 2 , so G K = 3 2 J G .
Since the ratio of the base of parallelogram A B C D to the base of parallelogram A B I H is A H A D = J L J K = J G + G L J G + G K = 2 J G J G + 3 2 J G = 6 5 , and since the area of parallelogram A B I H = 4 ⋅ 2 7 = 1 0 8 , the area of parallelogram A B I H is 6 5 ⋅ 1 0 8 = 9 0 .
Therefore, the area of the yellow region of parallelogram A B C D is 9 0 − 2 7 − 1 2 = 5 1 .
Since A B C D is a parallelogram, we can conclude that ∠ A B G = ∠ G E F and ∠ B A G = ∠ G F E due to the angles of parallel lines. Thus, △ A B G is similar to △ E F G because all three interior angles in both triangles are equal.
Hence, the area ratio between these similar triangles A B G : E F G equals 2 7 : 1 2 or 9 : 4 . Given the base length ratio of A B : E F be k , the height ratio of the bigger to smaller triangles will also be k . In other words, the area ratio then is in terms of base b and height h 2 1 × k b × k h : 2 1 × b × h or simply k 2 .
Hence, k 2 = 4 9 . Thus, k = 2 3 .
Then by creating a new parallel line H I passing the point G , the length ratio A I : I D = 3 : 2 , expressed as k earlier. Furthermore, with H I / / A B , A B H I is also a parallelogram and so has twice the area as △ A B G : the area of A B H I = 2 × 2 7 = 5 4 .
Also, we also obtain that A I : A D = 3 : 5 from the previous finding, and then the area ratio, with height s relative to A D , of A B H I : A B C D = s × A I : s × A D = 3 : 5 . Therefore, the area of A B C D = 3 5 × 5 4 = 9 0 .
Finally, the yellow region has area of 9 0 − 2 7 − 1 2 = 5 1 .