Parallelograms
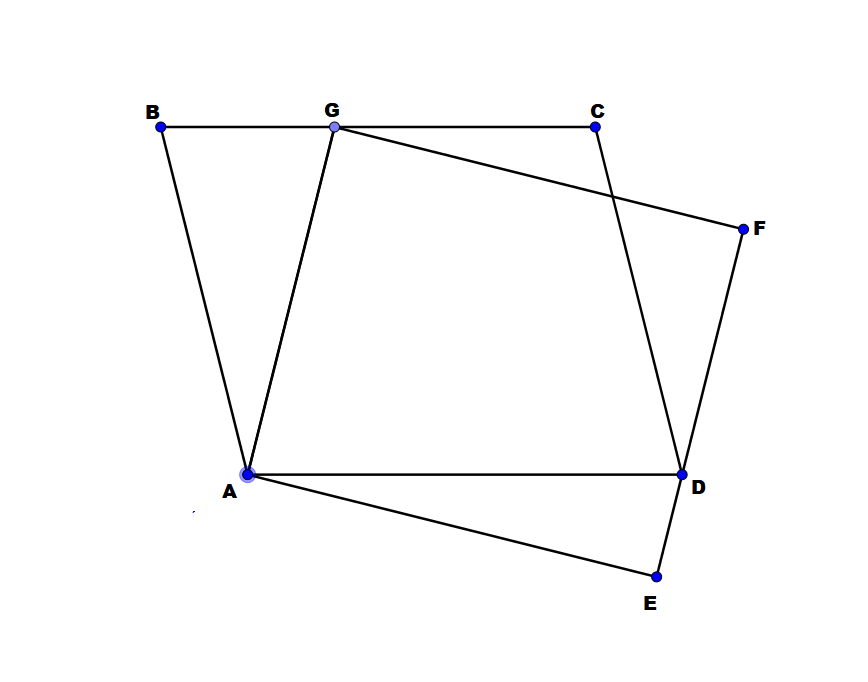
In image above, and are paralellograms. If the area of parallelogram is 20, what is the area of parallelogram ?
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Parallelograms may be replaced by rectangles with the same area and same relationship between vertices and parallel lines, so that the relationship needs only to be proven for rectangles.
Area of rectangle A B C D = a ( b + c )
Area of rectangle A E F G = a 2 + b 2 × x
From similarity of triangles A E B and D A H we get x y = a b or y = a b x
From Pythagorean theorem in triangle A H D : x 2 + y 2 = x 2 ( 1 + a 2 b 2 ) = ( b + c ) 2
Solving for x we get x = a 2 b 2 + 1 b + c
Substituting that into the formula for area of rectangle A E F G we get
[ A E F G ] = a 2 + b 2 × a 2 b 2 + 1 b + c = a 2 + b 2 × a 1 × a 2 + b 2 b + c = a ( b + c )
So the areas are the same size.