Parallelogramania

InΔADE m(∠A)=180-2θ as AD = AE ...... SAME WAY : m(∠B)=180-2α but from the properties of parallelogram that the sum of two adjacent angles equals to 180 therefore α+θ=90 therefore the required angle = 90

Because in triangle DEC, the median from E is the half of side DC. So: $\angle{DEC}=\boxed{90}$

∠A=2α ; ∠B=2θ => 2α + 2θ =180 => α + θ =90

∠AED =(180 - 2α )/2 = 90 - α ∠DEC =(180 - 2θ ) /2 = 90 - θ

∠DEC =180 - (∠AED+∠BEC )

∠DEC =180 - (90- α + 90- θ )

∠DEC = α + θ =90

u can consider abcd as a rectangle and get the same answer. ade and bce are then right isosceles triangles making dec a right angle(180-(45+45)).

As AB=2AD or AB/2=AD,E is the midpoint of AB so AE=AB/2.So AE=AD,the same way BE=BC(as its a parallelogram),so then ADE=AED and ECB=CEB.Now in triangle ADE....DAE+AED+ADE=180 or DAE+2 * AED=180........(1) and in triangle BCE...EBC+BEC+BCE=180 or EBC+2 * BEC=180......(2),Adding both (1) and (2) DAE+EBC+2 * AED+2 * BEC=180+180 or 180+2 * EBC+2 * AED=360[As DAE and EBC are in the same side of 2 parallel sides] or 2 * (AED+EBC)=360-180 or AED+EBC=180/2 or AED+BEC=90.Now AEB=AED+EBC+DEC or 180=90+DEC so DEC=90(Ans)

draw a line EF parallel

then <DAE = <DFE &

<EBC =<EFC ............(1)

AD = EF = BC= AE = EB= DF= FC

NOW <DEC= <DEF+<CEF

<DEF = (180- <DFE)/2 = 90-(<DFE/2)

<CEF= (180- <EFC)/2 = 90-(<EFC/2)

<DAE+ < EBC =180 ......PROPERTY OF PARALLELOGRAM.......(2)

<DEC = 90-(<DFE/2)+90- (<EFC/2)

<DEC= 180-((<DFE+<EFC)/2) BUT <DFE + <EFC = 180 ...............FROM (1) &(2) <DEC = 180-(180/2) <DEC = 180-90 <DEC = 90

as 2 Sides DE , CE drawn from DC on Midpt. of AB ---Therefore DE=CE ,, Therefore base <s are equal in measure so , m<EDC=m<ECD ---Since CE , DE are medians Therefore they bisect vertex angle , so m<C = m<D (Their Halves Are Equal) ---Since m<D=m<B , m<C=m<A (Property of parallelogram) (Opposite Angles) ---Since Sum Of Angles of //gram = 360 degrees ---we have 4 angles so each angle is equal To 90 ---therefore m<ECD=m<EDC = 90/2 = 45 degrees

In Triangle DEC , Required angle = 180 - (45+45) = 90 --By the way , All who assumed that It's a Rectangle are Geniuses ! :D Because It's Really a rectangle :D In Another Way :- Using what I proved above Two Triangles at the side are congurent We can get the Required angle by using the straight angle 180 - ( 45+45 ) = 90

Add point F at midpoint of line DC and triangle EFB will also be equilateral. The angles of all 4 equilateral triangles are 60 so DEF = 60 and parallelogram EFCB is bisected by line EC so angle FEC = 30. So angle DEC = DEF + FEC = 60 + 30 = 90.

As it is a parallelogram , AD=BC. And A/Q, AE=BE=AD, so DE=CE. Let ∠ADE=∠AED=∠BCE=∠BEC be x. As DE and CE bisect the angles ∠ADC and ∠BCD. Therefore, ∠CDE=∠DCE= x. As ABCD is a parallelogram , ∠ADC+∠BCD=180; 2x+2x=180; x=45. ∠DEC= 180-2x= 180-2(45)=90.

both angel d & c are parallel so if both are meeting to a common point which is also the mid point that turns into a 90 degree right triangle.

AD=BC=x, AB=2x. From definition of midpoint, AE=EB=x. AED is an isosceles triangle. BEC is also an isosceles triangle. From the definition of a parallelogram, A+B=180. The base angles of AED are 1/2 of 180-A or simply B/2. The base angles of BEC are 1/2 of 180-B or A/2. The angles around E add up to 180. DEC + A/2 + B/2=180. DEC+1/2(A+B)=180. DEC=90.

I actually solved it by intuition I just imagined those point A B C D in that parallelogram as hinges that allows rotation and DE, CE as elastic connections and tried to move it around with the consideration of ADE and CBE are isosceles triangles
I found out with this mental simulation that angle DEC actually remained constant and the two complementary angles at it's side are the ones changing So in a case of a rectangle it would be 90 degree I thought like a minute to confirm that theory geometrically with a more general form but nothing came to my mind and I was too lazy to search and refresh my information about parallelograms; so I just typed it :D

P.S: David's answer is just perfect (Y)

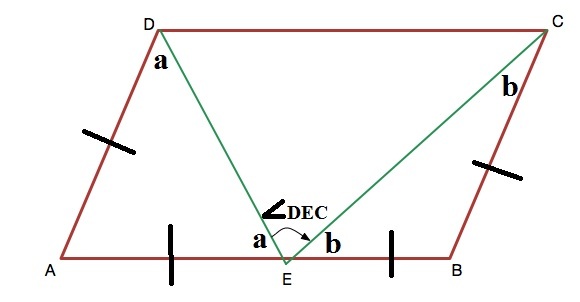
AD = AE = EB = BC because AB=2AD, E is midpoint, and opposite sides of a parallelogram are equal. With two isosceles triangles, we then have 2a=180-angle EAD and 2b=180-angle EBC=180-(180-angle EAD) since ABCD is a parallelogram. Since a+angle DEC+b=180, we have 2 times angle DEC = 360-2a-2b = 360 - (180-angle EAD) - (180-(180-angle EAD) = 180. Angle DEC = 90.

diagonals of rhombus bisects each other at 90 degrees

It is very clear that lines DE and CE are congruent since it shares the same vertex which is E and the figure is a parallelogram. Since the lines are congruent, then you can conclude that both lines DE and CE has the same angle. The angle to be find is in the figure of a triangle so it means the triangle is and Isosceles Triangle wherein the angles are 45-45-90 because of the midpoint E... The answer is 90...

With given details of AE =EB,and parallelogram angles,angle A + angle B =180 degree,therefore angle DEC will be 90 degree Ans K.K.GARg,India

if <ADE= x then, 4x+180=360 ; x=45, so, <DEC=2x=2*45=90 degree.

since no particulars, a parallelogram can be visualised a s a rectangle where point E is the mid point of longer side and thus in rectangle AD=AE, making each angled AED of 45 deg and also CEB of 45. basically there sum remains same i.e. 90, thus DEC is 90.

Its like a plane rectangle surface on which a shear force is applied distorting it into a paralleogram

Angles AEB=180 thefore angle 2E=(180) E=180/2 E=90

in the parallelogram let us say that side AD =x.then AE =x because AB=2x and E is the midpoint.let us say that angleADE =theta that implies angleDEA=theta because AD=AE that implies angleDAE=180-2(theta) that implies angleCBA =2(theta) because the sum of two adjacent angles of a parallelogram is 180 degrees.But BE=BC that implies angleCEB =90-(theta).Now i think u will be able to do it.